Introduktion till AVL-träd i datastruktur
AVL-träd i datastruktur hänvisar till Adelson, Velski & Landis Tree. Detta är en förbättrad version av det binära sökträdet. Det har alla funktioner från Binary Search Tree men skiljer sig bara eftersom de bibehåller en skillnad mellan höjden på det vänstra underträdet och det högra underträdet och säkerställer också att dess värde är <= 1 i trädet, detta kallas balans Faktor.
Balance Factor = height(left-subtree) − height(right-subtree)
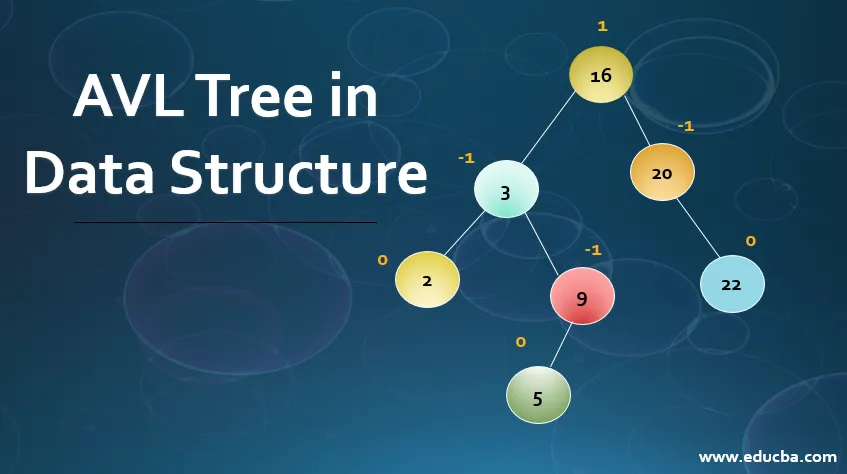
Till exempel: Tänk på följande träd

I exemplet ovan sägs höjden på höger underträd = 2 och vänster = 3 och därmed BF = 2 som är <= 1 och således sägs träd vara balanserat.
Varför behöver vi ett AVL-träd i DS?
När vi arbetar med Binary Search Tree, stöter vi på ett scenario där elementen är i sorterad ordning. I sådana fall är alla elementen i matrisen anordnade på en sida av roten, detta leder till en ökning av tidskomplexiteten för att söka efter ett element i en matris och komplexiteten blir- O (n) dvs värsta fallets komplexitet i trädet . För att lösa sådana problem och minska söktiden uppfanns AVL-träd av Adelson, Velski & Landis.
Exempel:

I figuren ovan var höjden på vänster undertråd = 3 som
Höjd på höger undertråd = 0
Således balansfaktor = 3-0 = 3. Således sökning efter ett element i ett sådant träd har O (n) av komplexitet som liknar linjär sökning. För att undvika det komplexa sökandet introducerades AVL-träd där varje nod i trädet måste underhållas
balansfaktor <= 1, annars ska olika rotationstekniker utföras för att balansera ett sådant träd.
Struct AVLNode
(
int data;
struct AVLNode *left, *right;
int ball factor;
);
Typer rotationer
När balansfaktorn för trädet inte uppfyller <= 1 villkoret måste rotationer utföras på dem för att göra det till ett balanserat träd.
Det finns fyra typer av rotationer:
1. Vänsterrotation: Om tillsatsen av en nod till höger om trädet gör det obalans måste i så fall Vänsterrotation utföras.
2. Höger rotation: Om tillägget av en nod till vänster om trädet gör nodens obalans måste högerrotation utföras. Med andra ord, när antalet noder ökar på vänster sida uppstår det ett behov av att flytta elementen till höger sida för att balansera det, så det sägs vara höger rotation.
3. Vänster-höger-rotation: Den här typen av rotation är en kombination av ovanstående två rotationer som förklaras. Denna typ av rotation inträffar när ett element läggs till till höger undertråd i ett vänster träd.
I ett sådant fall bör du först utföra vänsterrotation på undertråden följt av högerrotation av vänsterträdet.
4. Höger-vänster rotation: Denna rotationstyp består också av en sekvens med över 2 rotationer. Denna typ av rotation behövs när ett element läggs till vänster om höger undertråd och trädet blir obalanserat. I ett sådant fall utför vi först högerrotation på höger undertråd och sedan vänsterrotation på höger träd.
Verksamhet på AVL-träd i DS
Nedan tre operationer som kan utföras på AVL-trädet: -
1. Sök
Den här åtgärden liknar en sökning i Binary Search Tree. Stegen som följs är som nedan:
- Läs elementet som tillhandahålls av användaren säger x.
- Jämför elementet från roten, om det är detsamma, avsluta annars gå till nästa steg.
- Om x
Annars gå till rätt barn och jämför igen.
Följ processerna B och C tills du hittar elementet och avsluta.
Denna process har O (log n) komplexitet.
Exempel:
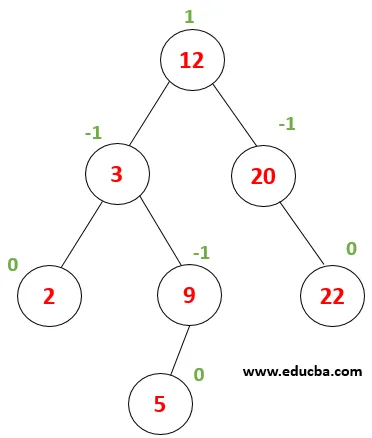 | Tänk på detta träd, där vi behöver utföra en sökning efter nodvärde 9. Låt först x = 9, rotvärde (12)> x, då måste värdet vara i den vänstra undertråden i rotelementet. |
 | Nu jämförs x med nodvärdet 3 x> 3 därmed måste vi fortsätta mot rätt undertråd. |
 | Nu jämförs x med nod (9), där 9 == 9 returnerar true. Således slutförs elementssökning i trädet. |
2. Insättning
När vi sätter in ett element i AVL-trädet, måste vi hitta platsen för det element som måste sättas in och sedan är elementet fäst på samma sätt som ett införande i BST, men efter det kontrolleras det om trädet fortfarande är balanserat eller inte dvs balansfaktorn för en nod är <= 1. Och speciella rotationer utförs vid behov.
Komplexiteten är O (log n).
Exempel: Betrakta trädet nedan,
 | Varje nod har en balansfaktor som 0, -1 eller 1 så trädet är balanserat. Låter nu vad som händer när en nod med värde 1 sätts in. Det första trädet korsas för att hitta platsen där det måste sättas in … 1 <2 är alltså skriven som ett vänster barn i noden (2). |
 | Efter införandet blir noden (9) obalans med en balansfaktor = 2. Nu utsätts den för höger rotation. |
 | Ett träd blir balans efter högerrotation och därmed är insättningsoperationen framgångsrik. |
3. Radering
Att radera ett element i AVL-trädet innefattar också att söka efter ett element i trädet och sedan ta bort det. Sökoperationen är densamma som BST, och efter att ha hittat elementet som ska raderas tas elementet bort från trädet och elementen justeras för att göra det BST igen. Efter det att dessa element har kontrollerat att de har en balansfaktor på 0, -1 eller 1 och därmed utförs lämpliga rotationer för att göra det balanserat.
Komplexitet om O (log n).
 | Tänk på det givna trädet, vars alla har en balansfaktor på 0, -1 eller 1. Låt oss nu ta bort en nod med värde 16. Det första trädet korsas för att hitta noden med värdet 16 samma som en sökande algoritm. |
 | Nod 16 kommer att ersättas med ordinarie föregångare för denna nod som är det största elementet från vänster undertråd, dvs 12 Trädet har blivit obalanserat och därför måste LL-rotation utföras. |
 | Nu har varje nod blivit balanserad. |
Slutsats - AVL-träd i datastruktur
AVL-trädet är en ättling till Binary Search Tree men övervinner dess nackdel med att öka komplexiteten om elementen sorteras. Den övervakar balansfaktorn för trädet till 0 eller 1 eller -1. I det fall att trädet blir obalanserat utförs motsvarande rotationstekniker för att balansera trädet.
Rekommenderade artiklar
Detta är en guide till AVL-träd i datastruktur. Här diskuterar vi Introduktion, operationer på AVL-träd i DS och typer av rotationer. Du kan också gå igenom våra andra relaterade artiklar för att lära dig mer–
- jQuery Elements
- Vad är datavetenskap
- Typer av träd i datastruktur
- C # Datatyper