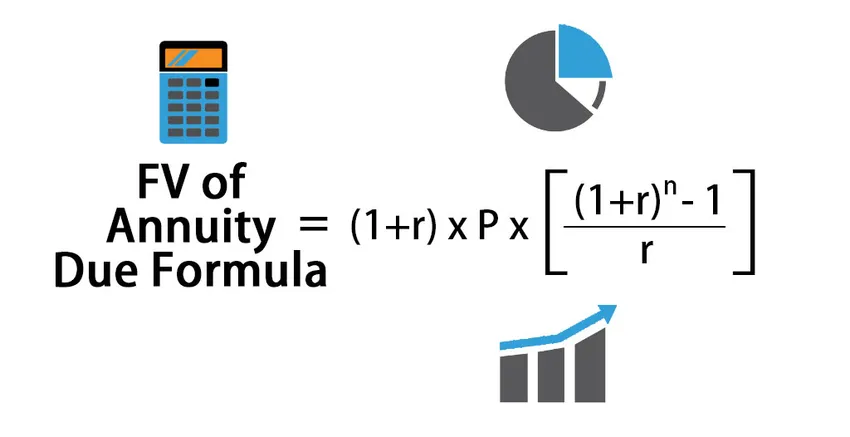
Framtida värde på formel för livränta (innehållsförteckning)
- Framtida värde på livränteformulär
- Exempel på framtida värde på formel för livränta (med Excel-mall)
- Framtida värde på beräkning för annuitet på grund av formel
Framtida värde på livränteformulär
Formeln för beräkning av Future Value of Annuity Due:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Var,
- P = periodisk betalning
- R = Rate per period
- N = Antal perioder
Exempel på framtida värde på formel för livränta (med Excel-mall)
Låt oss ta ett exempel för att förstå beräkningen av Future Value of Annuity Due på ett bättre sätt.
Du kan ladda ner denna framtida värde för livränta på grund av formel Excel-mall här - Framtida värde för annuitet på grund av formel Excel-mallExempel 1
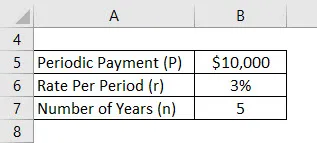
Låt oss anta att en Anand har deponerat 10 000 dollar per år och den effektiva kursen som hans konto erbjuder är 3%. Nu vill Anand beräkna sin framtida saldo efter 5 år med antagande av första insättningen från och med idag.
Lösning:
Framtida värde på livränta beräknas med hjälp av formeln nedan
FV of Annuity Due = (1 + r) * P * (((1 + r) n - 1) / r)
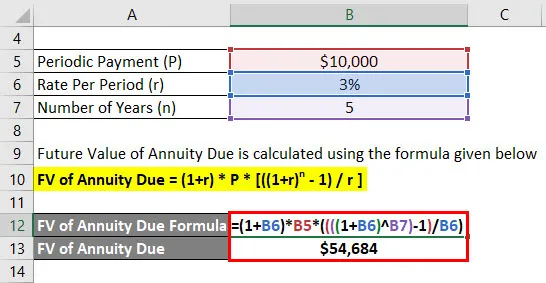
- FV of Annuity Due = (1+ 3%) * $ 10.000 * (((((1 + 3%) 5) - 1) / 3%)
- FV of Annuity Due = $ 54.684
Anand kommer att få 54 684 $ framtida balans efter 5 år.
Exempel 2
Låt oss anta att en Jagriti har deponerat 8 000 dollar per år och den effektiva kursen som hans konto erbjuder är 5%. Nu vill Jagriti beräkna sin framtida saldo efter 5 år med antagande av första insättningen från och med idag.

Lösning:
Framtida värde på livränta beräknas med hjälp av formeln nedan
FV of Annuity Due = (1 + r) * P * (((1 + r) n - 1) / r)
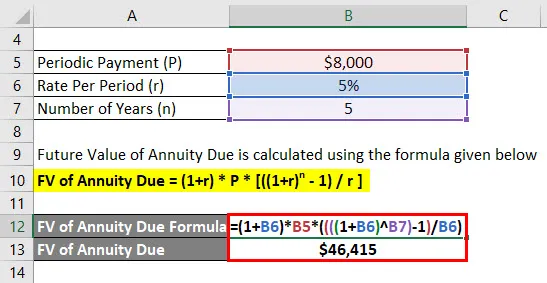
- FV of Annuity Due = (1+ 5%) * $ 8000 * (((((1 + 5%) 5) - 1) / 5%)
- FV of Annuity Due = $ 46.415
Jagriti kommer att få 46 415 $ framtida balans efter 5 år.
Exempel 3
Låt oss anta att en Anandriti har deponerat 20 000 dollar per år och den effektiva kursen som hans konto erbjuder är 2%. Nu vill Anandriti beräkna sin framtida saldo efter 5 år med antagande av första insättningen från och med idag.
Lösning:
Framtida värde på livränta beräknas med hjälp av formeln nedan
FV of Annuity Due = (1 + r) * P * (((1 + r) n - 1) / r)
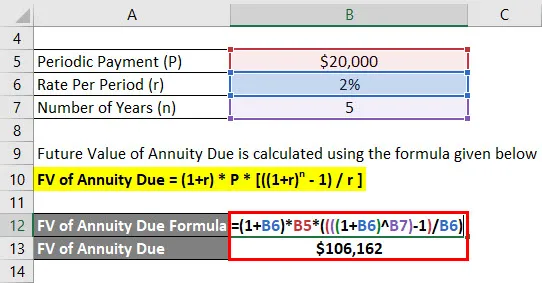
- FV of Annuity Due = (1+ 2%) * $ 20.000 * (((((1 + 2%) 5) - 1) / 2%)
- FV of Annuity Due = $ 1.06.162
Anandriti kommer att få $ 1.06.162 framtida balans efter 5 år.
Förklaring
För att beräkna slutvärdet för en serie av kassaflöden eller betalning där den första delen betalas direkt använder vi det framtida värdet på livränta. Den första omedelbara betalningen eller betalningen skiljer livränta på grund av den ordinarie livränta. En omedelbar eller omedelbar livränta kallas en förfallande livränta.
Det beräknar värdet på kassaflöden vid en framtida period. Användningen av FV för förfallodag är annorlunda i verkliga situationer än nuvärdet på en förfallen livränta. Anta till exempel att ett företag eller en person köper en livränta och har betalat den första delen i dag. Vi kan använda exemplet för att förklara ytterligare, anta att ett företag eller en person vill köpa en livränta från vem som helst och har gjort den första betalningen idag. För att beräkna det pris som ska betalas i denna situation kan vi använda nuvärdet på livränteformulär. Men om vi vill beräkna den återstående saldot efter att ha sparat ränta i fem år på kontot och vi beslutat att betala den första delen i dag, används i detta fall det framtida värdet på en livränta. Förfallande livränta kan förklaras som en typ av livränta där kassaflöden uppstår vid början av varje period. På grund av kassaflödenas avancerade karaktär är varje kassaflöde föremål för sammansättningseffekten för varje ytterligare period om det jämförs med en vanlig livränta. Det framtida värdet på en vanlig livränta är lägre än det framtida värdet på livränta eftersom det framtida värdet på livränta får en periodisk ränta på faktorn med ett plus.
Relevans och användningar av det framtida värdet av livränta
Låt oss förstå betydelsen av framtida värde och livränta separat. Framtida värde kan förklaras som det totala värdet för en summa kontanter som ska betalas i framtiden på ett specifikt datum. Och en livränta som förfaller kan förklaras som den serie betalningar som görs i början av varje period i regelbunden ordning. Därför kan framtida livränta förfallit förklaras som det totala värdet på ett angivet datum i framtiden för en serie systematiska / periodiska betalningar där betalningarna görs i början av varje period. Denna typ av transaktion och en sådan betalningsström kan ses för ett kontantmottagarkonto. Det totala värdet är det belopp som serien av betalningar som gjorts i det framtida datumet kommer att växa till, eftersom en viss ränta antas, och resultatet gradvis ökar under en viss period. Beräkningen av det framtida värdet på en vanlig livränta är identisk med detta men den enda skillnaden är att vi lägger till en extra betalningsperiod som görs i början.
Framtida värde på beräkning för annuitet på grund av formel
Du kan använda följande framtida värde för livräddningsberäknare
| P | |
| r | |
| n | |
| Framtida värde på livränteformulär | |
| Framtida värde på formel för livränta = | (1 + r) * P * (((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Rekommenderade artiklar
Detta har varit en guide till Future Value of Annuity Due Formula. Här diskuterar vi hur man beräknar Future Value of Annuity Due tillsammans med praktiska exempel. Vi erbjuder också Future Value of Annuity Due-kalkylatorn med nedladdningsbar Excel-mall. Du kan också titta på följande artiklar för att lära dig mer -
- Guide till formel för tidsvärde av pengar
- Exempel på nuvärdefaktorformler
- Kalkylator för informationsförhållande formel
- Formel för graden av driftshävstång