
F-testformel (innehållsförteckning)
- Formel
- exempel
Vad är F-testformel?
F-test är ett statistiskt test som hjälper oss att hitta om två populationsuppsättningar som har en normalfördelning av sina datapunkter har samma standardavvikelse eller variationer. Men det första och främsta att utföra F-test är att datasätten ska ha en normal distribution. Detta tillämpas på F-distribution under nollhypotesen. F-test är en mycket viktig del av analysen av variation (ANOVA) och beräknas genom att ta förhållanden mellan två varianter av två olika datamängder. Som vi vet att avvikelser ger oss informationen om spridningen av datapunkterna. F-test används också i olika test som regressionsanalys, Chow-test, etc.
Formel F-test:
Det finns ingen enkel formel för F-Test men det är en serie steg som vi måste följa:
Steg 1: För att utföra ett F-test måste vi först definiera nollhypotesen och alternativ hypotesen. Dessa ges av: -
- H0 (Nullhypotes): Variation av 1: e datauppsättning = Variation av en andra datauppsättning
- Ha: Variation av 1: e datauppsättning <Varians av 2: a datauppsättning (för ett lägre test med en svans)
- Ha: Variation av 1: e datauppsättning > Variation av en andra datauppsättning (för ett övre en-svansat test)
- Ha: Variation av 1: e datauppsättning ≠ Variation av en andra datauppsättning (för ett två-svansat test)
Steg 2: Nästa sak vi måste göra är att vi måste ta reda på graden av betydelse och sedan bestämma graden av frihet för både teller och nämnare. Detta hjälper oss att bestämma deras kritiska värden. Frihetsgraden är provstorlek -1.
Steg 3: F-testformel:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Steg 4: Hitta F-kritiska värdet från F-tabellen med en grad av frihet och nivå av betydelse.
Steg 5: Jämför dessa två värden och om ett kritiskt värde är mindre än F-värdet kan du avvisa nollhypotesen.
Exempel på F-testformel (med Excel-mall)
Låt oss ta ett exempel för att förstå beräkningen av F-Test på ett bättre sätt.
Du kan ladda ner denna F-TEST-formel Excel-mall här - F-TEST-formel Excel-mallF-testformel - exempel # 1
Låt oss säga att vi har två datauppsättningar A & B som innehåller olika datapunkter. Utför F-test för att avgöra om vi kan avvisa nollhypotesen på en 1% -nivå.
Datauppsättningar:
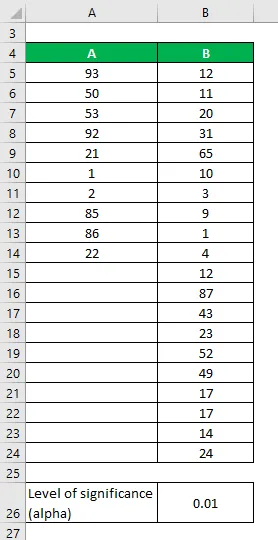
Lösning:
Nullhypotes: variant av A = variation av B
Grad av frihet beräknas som
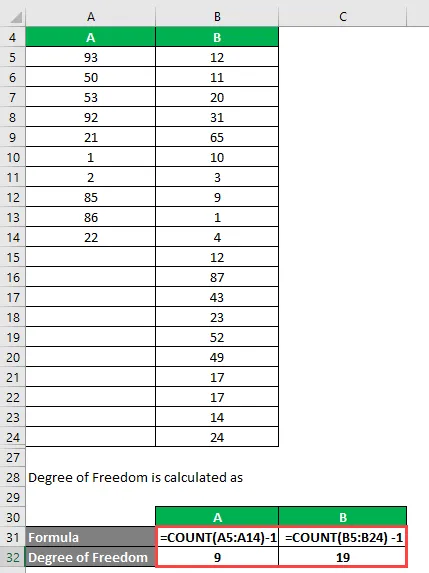
Grad av frihet
- För A = 10 - 1 = 9
- För B = 20 - 1 = 19
Variationen beräknas som:

- Varians av A = 1385, 61
- Varians av B = 521, 22
F-värdet beräknas med hjälp av formeln nedan
F-värde = variant av 1: a Datauppsättning / variant av 2: a datauppsättning
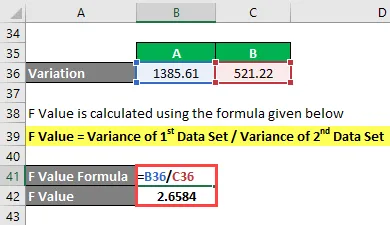
- F-värde = 1385, 61 / 521, 22
- F-värde = 2.6584
F-tabell:
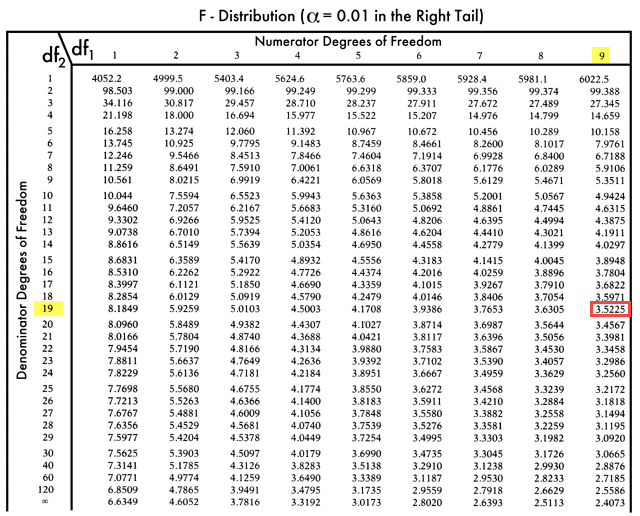
Så F kritiska värde = 3, 5225
Eftersom F kritiskt är större än F-värdet kan vi inte avvisa nollhypotesen.
F-testformel - exempel # 2
Anta att du arbetar i ett forskningsföretag och vill att nivån på koldioxidutsläpp sker från två olika cigarettmärken och om de skiljer sig väsentligt eller inte. I din analys har du samlat in följande information:
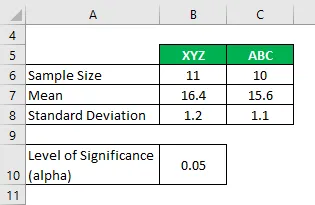
Lösning:
Grad av frihet beräknas som
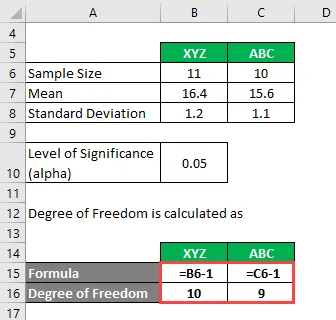
Grad av frihet
- För XYZ = 11 - 1 = 10
- För ABC = 10 - 1 = 9
Variationen beräknas som:
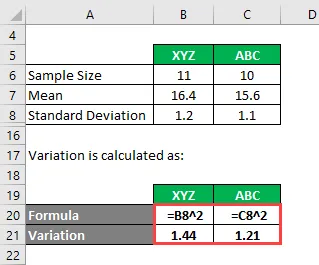
- Variation av XYZ = 1, 2 2 = 1, 44
- Varians av ABC = 1, 1 2 = 1, 21
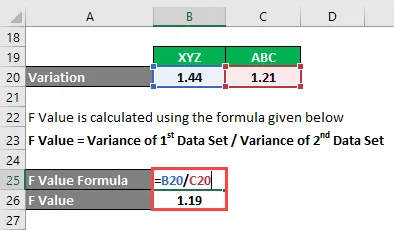
- F-värde = 1, 44 / 1, 21
- F-värde = 1, 19
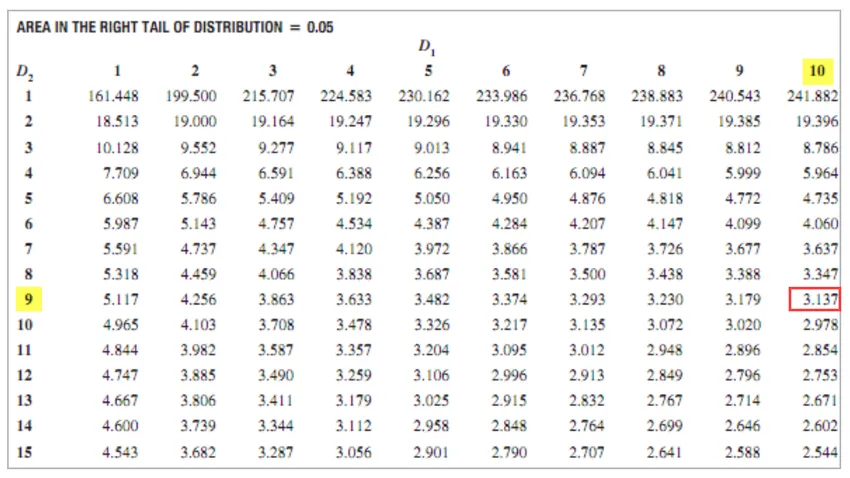
F Kritiskt värde = 3.137
Eftersom F-kritiskt> F-värde kan nollhypotesen inte avvisas.
Förklaring
I exemplen ovan har vi sett tillämpningen av F-Test och hur det utförs. Men det finns en uppsättning antaganden vi måste ta hand innan vi utför F-test annars kommer vi inte att få erforderliga resultat:
- Det första är att vi alltid måste placera tallen för högre variansvärde medan vi beräknar F-värdet. Så om F = V1 / V2, bör V1 vara> V2
- Om vi vill utföra 2 halstest måste vi dela upp signifikansnivån med 2 och det kommer att vara rätt nivå för att hitta det kritiska värdet
- Vi använder bara varians är F-värdet beräkning och om vi ges med standardavvikelser, som i exempel 2, måste de vara kvadratiska för att hitta variansen.
- Båda proverna bör vara oberoende av varandra och provstorleken bör vara mindre än 30
- Befolkningsuppsättningar för vilka proverna tas ut måste normalt distribueras
Dessa är de viktigaste parametrarna / antagandet som bör tas om hand när du utför F-Test.
Relevans och användning av F-testformler
F-test, som diskuterats ovan, hjälper oss att kontrollera om de två befolkningsvariationerna är jämställda. Så när vi har två oberoende prover som dras från en normal population och vi vill kontrollera om de har samma variation eller inte, använder vi F-test. F-test har också stor relevans vid regressionsanalys och även för att testa betydelsen av R2. Så i ett nötskal är F-Test ett mycket viktigt verktyg i statistik om vi vill jämföra variationen på 2 eller fler datasätt. Men man bör ha alla antaganden i åtanke innan man utför detta test.
Rekommenderade artiklar
Detta har varit en guide till F-Test Formula. Här diskuterar vi hur man beräknar F-Test tillsammans med praktiska exempel och nedladdningsbar Excel-mall. Du kan också titta på följande artiklar för att lära dig mer -
- T-distributionsformel
- Formel för prissättning på obligationer
- Procentfelformel
- Beräkning av NOPAT-formeln