Vektorer i Matlab - Typer av vektordrift med exempel

Introduktion till vektorer i Matlab

En vektor är en sluten uppsättning element. I Matlab kan vi skapa vektorer med fyrkantiga parenteser. Vektorer är en av illustrationerna av matriser (endimensionell matris). det kan representeras på två sätt radvektor och kolumnvektor.

Radvektor

Det är horisontella uppsättning element. Det representeras inom fyrkantiga parenteser. Varje element separeras med komma eller rymd.

X = (4 7 8) eller X = (4, 7, 8)

Kolumnvektor

Det är en vertikal uppsättning element. Det representeras också inom fyrkantiga parenteser. Det finns två sätt att skapa kolumnvektorer först är att separera varje element med en semikolon och ett annat sätt är att skriva varje element på nästa rad i kommandofönstret.

X = (4; 6; 7) eller

X = (4

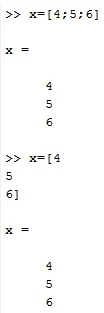
Vektoroperationer

Vektoroperatörer klassificeras i stort sett i två kategorier.

1. Aritmetisk operation

Låt oss betrakta två vektorer x och y med värden x = (1 4 5 3) och y = (5 3 2 1) vi kan utföra olika operationer på dessa två vektorer x och y.

a. Multiplikation: Denna funktion används för att multiplicera med valfritt aritmetiskt värde till hela vektorn.

Till exempel:

mul = 3 * x

mul = 3 * (1 4 5 3)

mul = (3 12 15 9)

Syntax: variable name = arithmetic constant * vector name

b. Trigonometrisk funktion: Vi kan tillämpa vilken trigonometrisk funktion som helst på vektorliknande synd, cos, solbränna, cosec, sec etc.

Exempel tri = cos (x)

Svaret är: 0, 54 - 0, 65 0, 28 -0, 99

Syntax: variable name = trigonometric function name ( vector name )

Summa: Detta visar totalt (tillägg av) hela element i en vektor.

Exempel

x = (1 4 5 3)

Totalt = summa (x)

Utgången är totalt = 13

Syntax: variable name = = sum ( vector name )

c. Längd: Den visar längden på en viss vektor, låt oss en vektor p = (9 7 5 3 1 9 7 5 3 1)

Exempel

p = (9 7 5 3 1 9 7 5 3 1)

Len = längd (p)

Utmatningen är Len = 10

d. Tillsats av vektorer: Tillsats av två eller flera vektorer är enkel operation i Matlab, låt oss betrakta två vektorer p och q.

P = (4 6 3 2) och q = (5 7 9 1)

Lägg till = p + q

Output är Add = (9 13 12 3)

Syntax: vector name operator ( + ) vector name

På liknande sätt kan vi göra subtraktionsoperationer som sub = p - q

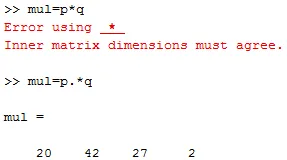
e. Multiplikation av vektorer: Om vi vill göra multiplikation av två vektorer fungerar inte en enkel multiplikationsoperatör (*). Därför måste vi lägga till en punktoperator ('.') Med en multiplikationsoperatör.

Exempel:

P = (4 6 3 2) och q = (5 7 9 1)

mul = p. * q

utgången är mul = (20 42 27 2)

Syntax: variable name = vector name dot operator multiplication operator vector name

Anta att jag vill ta reda på kvadratet för en viss vektor eller att jag bara vill multiplicera vektorn med den vektorn.

Sedan kommer syntaxen att vara squr = x. 2

2. Relationell operation

a. Lika med operatören : denna operatör jämför varje n varje element från två vektorer och ger utdata är noll och en form.

Exempel

m = (2 5 8)

Och n = (5 5 3)

Som vi vet finns det tre element i vektor m och vektor n,

m == n

Ovanstående uttalande ger utdata som 0 1 0, vilket innebär att första nej inte är lika, det andra numret är lika och det tredje nej är inte lika. O representerar falskt och 1 representerar sant.

b. Mindre än operatören (<): Mindre än operatören representerar med symbolen '<'. vi kan jämföra en given matris med någon aritmetisk konstant eller med någon annan vektor.

Exempel

m = (3 2 4)

n = (1 1 1)

m <n

utgången kommer att vara 0 0 0, det betyder att alla siffror är större än vektorn n.

och om m <10

då blir utgången 1 1 1, det betyder att alla siffror är mindre än 10.

c. Större än operatör (>): Större än operatören representerar med symbolen ('>'). Vi kan jämföra en given matris med vilken aritmetisk konstant som helst eller med någon annan vektor.

Exempel:

M = (3 2 4)

N = (1 1 1)

m> n

Output kommer att vara 1 1 1, det betyder att alla värden är större än värdena på vektor n.

Slutsats - vektorer i Matlab

I Matlab kan vi skapa olika typer av vektorer där vi kan utföra olika operationer som tillägg, subtraktion, multiplikation, kvadrat, kvadratrot, kraft, skalning, vektormultiplikation, punktprodukt etc.

Rekommenderade artiklar

Detta är en guide till vektorer i Matlab. Här diskuterar vi de typer av vektordrift som inkluderar aritmetisk och relationell operation tillsammans med några exempel. Du kan också titta på följande artiklar för att lära dig mer -