Effektiv årskursformel (innehållsförteckning)
- Formel
- exempel
- Kalkylator
Vad är den effektiva årliga kursformeln?
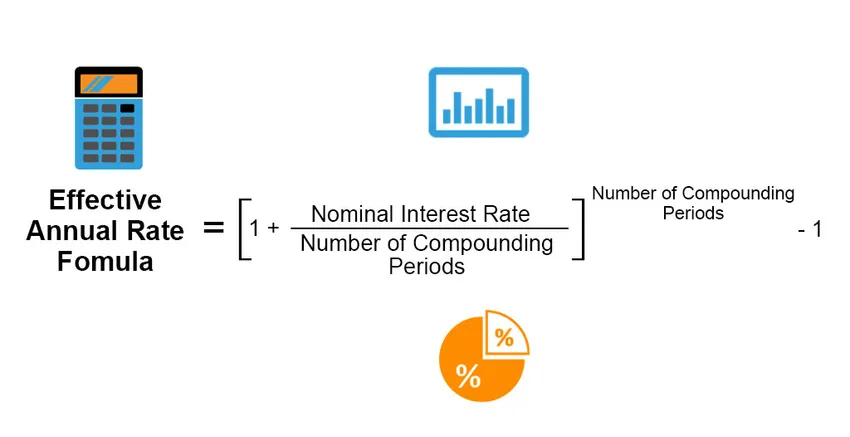
Effektiv årsränta är den faktiska räntan som tjänas eller betalas ut på en investering, lån eller någon liknande finansiell produkt, och den skiljer sig annars från ”nominell ränta” på grund av utbetalningsperioden för ränta, sammansättning av räntesats, totalt lånets eller investeringens tidsperiod, etc. Effektiv årskurs beräknas med följande formel;
Effective Annual Rate = ((1 + (Nominal Interest Rate / Number of Compounding Periods)) Number of Compounding Periods) – 1
Exempel på effektiv årlig kursformel (med Excel-mall)
Låt oss ta ett exempel för att förstå beräkningen av effektiv årskurs på ett bättre sätt.
Du kan ladda ner denna effektiva årliga kursformel Excel-mall här - Effektiv årlig kursformel Excel-mallEffektiv årskursformel - exempel # 1
Anta att en herr X tar ett personligt lån från en bank med en ränta på 20%, sammansatt halvårsvis. Beräkna effektiv årskurs med hjälp av informationen.

Lösning:
Effektiv årskurs beräknas med hjälp av formeln nedan
Effektiv årskurs = ((1 + (nominell räntesats / antal sammansatta perioder)) Antal sammansatta perioder) - 1

- Effektiv årskurs = ((1 + (20% / 2)) 2) - 1
- Effektiv årskurs = 21%
Effektiv årskursformel - exempel # 2
Anta att Mr. A investerade 100 $ i ett insättningsintyg som betalar ut en nominell årlig ränta på 10% sammansatt kvartalsvis. Beräkna den effektiva årliga räntan.

Lösning:
Effektiv årskurs beräknas med hjälp av formeln nedan
Effektiv årskurs = ((1 + (nominell räntesats / antal sammansatta perioder)) Antal sammansatta perioder) - 1
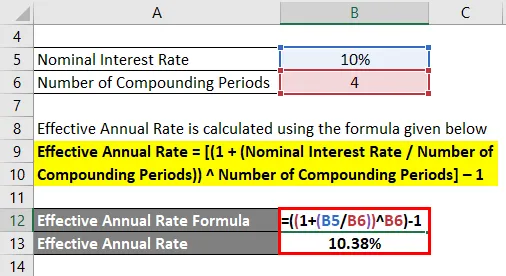
- Effektiv årskurs = ((1 + (10% / 4)) 4) - 1
- Effektiv årskurs = 10, 38%
Effektiv årskursformel - exempel # 3
Låt oss anta att investeringsfonderna får 15, 50% årlig ränta som intäkter, medan P2P-utlåningen tjänar 15% årlig nominell ränta, sammansatt varje månad. Så beräkna den effektiva årliga räntan för båda fallen.

Lösning:
Effektiv årskurs beräknas med hjälp av formeln nedan
Effektiv årskurs = ((1 + (nominell räntesats / antal sammansatta perioder)) Antal sammansatta perioder) - 1
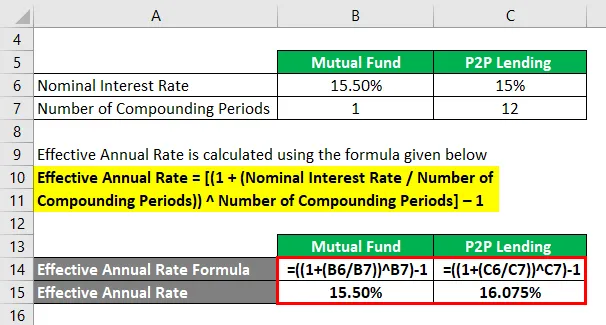
För ömsesidig fond
- Effektiv årskurs = ((1 + (15, 50% / 1)) 1) - 1
- Effektiv årskurs = 15, 50%
För P2P-utlåning
- Effektiv årskurs = ((1 + (15% / 12)) 12) - 1
- Effektiv årskurs = 16, 075%
Förklaring
Den nominella räntan är den angivna räntan på den finansiella produkten. I exempel 3 får den nominella räntan som visas på produkterna den fond som ser ut som det föredragna valet av investeringar för investerare på grund av den 0, 50% högre årliga nominella räntesatsen.
Den effektiva årliga räntan beräknas emellertid genom att ta den nominella årliga räntan och sammansätta den för antalet angivna perioder (12 om sammansättningen är månatlig, 6 om sammansättningen är tvåmånaders, 4 om den är kvartalsvis och 2 om den är sammansatt är halvårsvis) tillämplig inom ett år. När det gäller fonder är antalet sammansatta perioder per år 1, medan det gäller P2P-utlåning är det månatligt sammansatt, varför det finns 12 sammansättningsperioder.
Baserat på formeln,
Effektiv årlig avkastning = ((1 + (nominell ränta / antal sammansatta perioder)) (antal sammansatta perioder)) - 1
Effektiv årlig avkastning på fonderna (((1 + (15, 50% / 1)) 1) - 1 = 15, 50%
P2P-utlåning Effektiv årlig avkastning = ((1 + (15, 00% / 12)) 12) - 1 = 16, 075%
Relevans och användningar av effektiv formel för årlig ränta
Den effektiva årliga ränteformeln används för att skilja den faktiska IRR (Intern avkastningskurs) eller en årlig avkastning för en ränta som kan eller inte kan blandas flera gånger under en viss period. Detta kan mycket väl användas för att jämföra olika typer av investeringsmöjligheter eller lånefaciliteter som tas under olika strukturer.
Låt oss anta att det finns två investeringsmöjligheter, postperiodens inlåning och fasta bankdepositioner som en investerare har minskat till, med tanke på hans / hennes riskaptit och lämplighet. Investerarens slutliga mål är att få ut mesta möjliga av dessa insättningar och tjäna en högre avkastning. Båda instrumenten erbjuder emellertid något olika räntesatser, medan Post Office Term Deposit erbjuder kvartalsvis sammansättning för den aktuella terminen.
- Investeringsbelopp: Rs. 10 lakhs
- Investeringsperiod: 5 år
- Fast bankdeposition: 7, 5% årligt ränta
- Kontorsperiod: 7, 4% årligt ränta, sammansatt kvartalsvis
Med hänsyn till de årliga räntorna som erbjuds verkar den fasta bankens inlåning vara det bättre alternativet. Men om investeraren faktiskt beräknar den kvartalsvisa sammansättningsfaktorn för Post Office Term Deposit, resulterar det i en effektiv årlig ränta / avkastning på 7, 61%.
På grund av denna lilla förändring från 7, 4% till 7, 61% i effektiv ränta skulle investeraren tjäna totalt Rs. 4, 42848, 28 från detta instrument, medan han / hon skulle ha tjänat Rs. 3, 35, 469, 14 från bankinstrumentet.
Om investeraren missar beräkningen av denna effektiva årliga ränta, skulle han / hon ha tappat bort möjligheten att vinna ungefär mer än Rs. 1 lakh från sin investering.
Effektiv beräkning för årlig kursformel
Du kan använda följande effektiva årliga räknemaskin
| Nominell ränta | |
| Antal sammansatta perioder | |
| Effektiv årskurs | |
| Effektiv årskurs = | ((1 + (nominell räntesats / antal sammansatta perioder)) Antal sammansatta perioder ) - 1 | |
| ((1 + (0/0)) 0 ) - 1 = | 0 |
Rekommenderade artiklar
Detta är en guide till effektiv årlig kursformel. Här diskuterar vi hur man beräknar effektiv årskurs tillsammans med praktiska exempel. Vi tillhandahåller också en effektiv årskursräknare med nedladdningsbar Excel-mall. Du kan också titta på följande artiklar för att lära dig mer -
- Kalkylator för formel för realränta
- Avkastning på sysselsatt kapitalformel | Definition
- Hur beräknar jag den effektiva räntan?
- Vad är nuvärdet av livränteformeln?