Introduktion till Heap Sort in C
Sortering är en teknik som handlar om beställning av element baserat på olika egenskaper. (Egenskaper som att ordna data i stigande, fallande eller alfabetiska ordningar). Ett viktigt exempel på sortering som vi kan tänka på här är att beställa varor under online-shopping. Vi kan relatera till priser, popularitet, senaste och så vidare. Så det finns många tekniker för att placera element genom sortering. I det här ämnet kommer vi att lära oss om Heap Sort i C.
Här kommer vi att lära oss en av de vanligaste sorteringsteknikerna, Heap Sort, genom C-programmeringsspråk.
Logiken för Heap Sort
Hur kan vi faktiskt utföra heap sortering? Låt oss kolla nedan.
För det första är högen en av den trädbaserade datastrukturen. Det här trädet är alltid ett komplett binärt träd. Och det finns två slags hög
- Min - Heap: Vanligtvis arrangerat i stigande ordning, det vill säga om det överordnade nodelementet har ett värde som är mindre än det för barnnodelement.
- Max - Heap: Vanligtvis arrangerat i fallande ordning, det vill säga om överordnade nodelement har ett värde som är mer än för barnnodelement.
Steg för Heap Sort
- När en osorterad listdata har erhållits, organiseras element i heapdatastrukturen antingen baserat på att skapa en min-heap eller en max-heap.
- Det första elementet från listan ovan läggs till i vårt array
- Återigen bildar huvuddatatstrukturstekniken densamma som det första steget och följs återigen antingen det högsta elementet eller det minsta elementet och läggs till i vårt array.
- Upprepade steg hjälper oss att få matrisen med den sorterade listan.
Program för Heap Sort in C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Först ber vi användaren att mata in antalet element som tas för sortering och sedan får användaren ange olika element som ska sorteras.
Steg följs
- Det nästa som vi fokuserar på är att skapa en höguppsättning, i detta fall maxuppsättning.
- Det huvudsakliga villkoret för att få en maxheap-grupp är att kontrollera att inget föräldernodvärde är mindre än dess barndodvärde. Vi kommer att byta tills vi når det villkoret.
- Den huvudsakliga fördelen med detta kompletta binära träd är att de vänstra och högra barnnoderna i en överordnad nod kan nås med värdena 2 (i) + 1 och 2 * (i) + 2-värden. Där jag är föräldernoden.
- Så på det sättet här placerar vi vår rotnod som innehåller det maximala värdet på det högsta bladnodplatsen. Och sedan igen efter samma procedur så att nästa maximala nummer nu blir rotnoden.
- Vi kommer att följa samma procedur tills bara en nod är kvar i höguppsättningen.
- Och sedan ordnar vi vår höguppsättning för att bilda en perfekt sorterad matris i ökande ordning.
- Slutligen skriver vi ut den sorterade matrisen i utdata.
Produktion:
Utgången bifogas nedan.
Låt mig visa dig den bildliga bilden av händelserna:
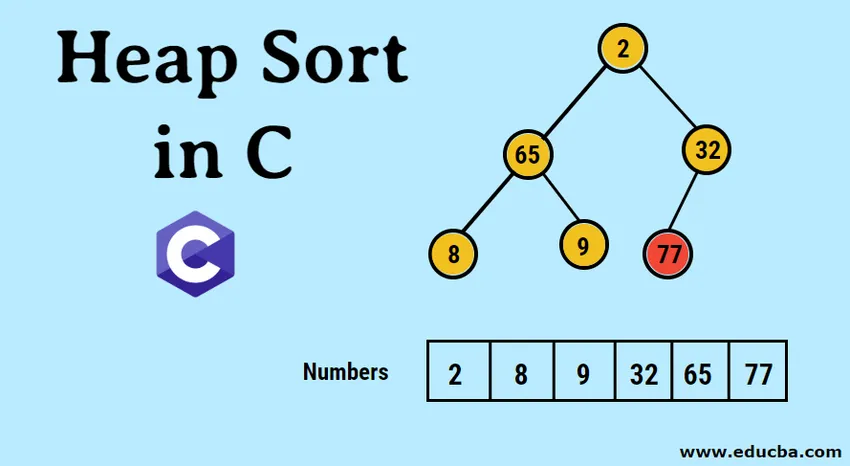
- De inmatade uppgifterna representeras först i form av en en-dimensionell matris enligt följande.

- Bildbilden av det bildade binära trädet är som följer:
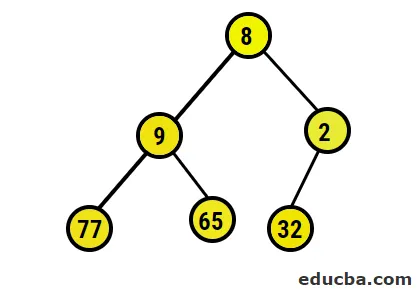
- Nu ska vi konvertera till maxheapen genom att se till att alla överordnade noder alltid är större än underordnade noder. Som nämnts i utgången under heap-sorterad matris, skulle bildbilden vara:
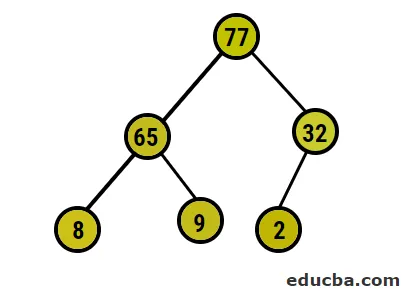
- Efter detta kommer vi att byta rotnoden med den extrema bladnoden och sedan ta bort den från trädet. Bladnoden skulle vara roten nu och igen samma process som följdes för att återigen få det högsta elementet i roten
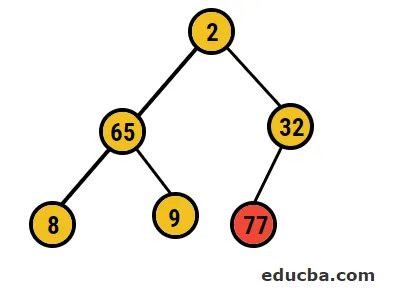
- Så i detta fall raderas 77 siffror från detta träd och placeras i vårt sorterade array och processen upprepas.
Ovanstående har vi sett det för att bilda max höguppsättning. Samma process hanteras också med bildningen av min-heap array. Som diskuterats ovan är den enda skillnaden i förhållandet mellan förälder och barn nodelement.
Kan du som en övning prova att bilda högen i fallande ordning?
Slutsats
Även om det finns många sorteringstekniker, anses heap sortering vara en av de bättre sorteringsteknikerna på grund av dess tid och rymdkomplexitet. Tidskomplexiteten för alla bästa, genomsnittliga och värsta fall är O (nlogn), där värsta fall är bättre än värsta fallskomplexiteten för Quicksort och rymdkomplexiteten är O (1).
Rekommenderade artiklar
Detta är en guide till Heap Sort i C. Här diskuterar vi logiken och Stegen för Heap Sort med provkoden och utdata tillsammans med bildföreställningar. Du kan också titta på följande artiklar för att lära dig mer -
- Heap Sort In Java
- Urval Sortera i Java
- Palindrome in C-programmet
- Mönster i C-programmering
- Heap Sortera i C ++ (algoritm)
- Heap Sort i Python
- C Programmering av matrismultiplikation