
Marginal of Error Formula (Innehållsförteckning)
- Marginal of Error Formula
- Exempel på marginal för felformel (med Excel-mall)
- Marginal of Error Formula Calculator
Marginal of Error Formula
I statistik beräknar vi konfidensintervallet för att se var värdet på data från provstatistik kommer att falla. Området värden som ligger under och över provstatistiken i ett konfidensintervall kallas Margin of Error. Med andra ord är det i princip graden av fel i provstatistiken. Högre felmarginal, desto mindre kommer förtroendet för resultaten eftersom graden av avvikelse i dessa resultat är mycket hög. Som namnet antyder är felmarginen ett värdeintervall över och under de faktiska resultaten. Om vi till exempel får ett svar i en undersökning där 70% människor har svarat "bra" och felmarginal är 5%, betyder detta att i allmänhet 65% till 75% av befolkningen tycker att svaret är "bra" .
Formeln för Margin of Error -
Margin of Error = Z * S / √n
Var:
- Z - Z-poäng
- S - Standardavvikelse för en befolkning
- n - Provstorlek
En annan formel för beräkning av felmarginal är:
Margin of Error = Z * √((p * (1 – p)) / n)
Var:
- p - Provproportion (bråkdel av provet som är en framgång)
För att hitta önskad z-poäng måste du känna till provets konfidensintervall eftersom Z-poäng är beroende av det. Nedanstående tabell ges för att se förhållandet mellan ett konfidensintervall och z-poäng:
| Konfidensintervall | Z - Poäng |
| 80% | 1, 28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
När du vet konfidensintervallet kan du använda motsvarande z-värde och beräkna felmarginalen därifrån.
Exempel på marginal för felformel (med Excel-mall)
Låt oss ta ett exempel för att förstå beräkningen av Margin of Error på ett bättre sätt.
Du kan ladda ner denna marginal för fel mall här - marginal av fel mallMarginal of Error Formula - Exempel # 1
Låt oss säga att vi gör en undersökning för att se vilken betyg som universitetsstudenter får. Vi har valt 500 elever slumpmässigt och frågat deras betyg. Genomsnittet för detta är 2, 4 av 4 och standardavvikelsen är säga 30%. Antag att konfidensintervallet är 99%. Beräkna felmarginalen.
Lösning:
Marginal of Error beräknas med hjälp av formeln nedan
Felmarginal = Z * S / √n
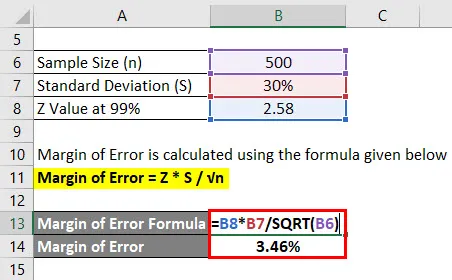
- Felmarginal = 2, 58 * 30% / √ (500)
- Felmarginal = 3, 46%
Detta innebär att med 99% förtroende är medelvärdet för eleverna 2, 4 plus eller minus 3, 46%.
Marginal of Error Formula - Exempel # 2
Låt säga att du lanserar en ny hälsoprodukt på marknaden men du är förvirrad vilken smak människor gillar. Du är förvirrad mellan banansmak och vaniljsmak och har beslutat att göra en undersökning. Din befolkning för det är 500 000 vilket är din målmarknad och utifrån det beslutade du att fråga yttrandet från 1000 personer och det kommer urvalet. Antag att ett konfidensintervall är 90%. Beräkna felmarginalen.
Lösning:
När undersökningen är klar, fick du veta att 470 personer gillade banansmaken och 530 har bett om vaniljsmak.
Marginal of Error beräknas med hjälp av formeln nedan
Felmarginal = Z * √ ((p * (1 - p)) / n)
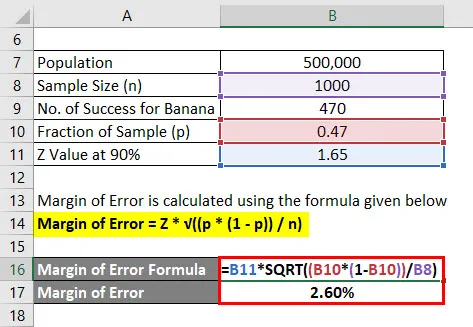
- Felmarginal = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Felmarginal = 2, 60%
Så vi kan säga att med 90% förtroende för att 47% av alla människor gillade banansmak plus eller minus 2, 60%.
Förklaring
Som diskuterats ovan hjälper felmarginalen oss att förstå om provstorleken för din undersökning är lämplig eller inte. Om marginalfelet är för stort kan det vara så att vår provstorlek är för liten och vi måste öka det så att provresultaten matchar närmare beståndsresultaten.
Det finns några scenarier där felmarginalen inte kommer att vara till stor nytta och inte hjälper oss att spåra felet:
- Om frågorna i undersökningen inte är utformade och inte hjälper till att få önskat svar
- Om de personer som svarar på undersökningen har en viss förspänning angående den produkt som undersökningen görs för, är resultatet också inte riktigt
- Om det valda urvalet är den rätta representanten för befolkningen, kommer i så fall också resultaten att vara långt ifrån.
Här är också ett stort antagande att befolkningen normalt är fördelad. Så om provstorleken är för liten och befolkningsfördelningen inte är normal kan z-poäng inte beräknas och vi kan inte hitta felmarginal.
Relevans och användning av formelmarginal
När vi använder provdata för att hitta ett relevant svar för den uppsatta befolkningen finns det viss osäkerhet och chanser att resultatet kan avvika från det faktiska resultatet. Felmarginalen kommer att säga oss att vad som är nivån för avvikelsen är det är provutgången. Vi måste minimera felmarginalen så att våra provresultat visar den faktiska historien om befolkningsdata. Så lägre felmarginal, bättre blir resultaten. Felmarginalen kompletterar och kompletterar den statistiska information som vi har. Om till exempel en undersökning visar att 48% av befolkningen föredrar att spendera tid hemma under helgen, kan vi inte vara så exakta och det finns några saknade element i den informationen. När vi införde en felmarginal här, säg 5%, kommer resultatet att tolkas som 43-53% människor gillade idén att vara hemma under helgen, vilket är fullständigt meningsfullt.
Marginal of Error Formula Calculator
Du kan använda följande Margin of Error Calculator
| Z | |
| S | |
| √n | |
| Felmarginal | |
| Felmarginal | = |
|
|
Rekommenderade artiklar
Detta har varit en guide till formeln Margin of Error. Här diskuterar vi hur man beräknar felmarginalen tillsammans med praktiska exempel. Vi erbjuder också en marginal av felkalkylatorn med nedladdningsbar Excel-mall. Du kan också titta på följande artiklar för att lära dig mer -
- Guide till formel för direkt avskrivning
- Exempel på fördubblingstidsformel
- Hur man beräknar amortering?
- Formel för central begränsningssats
- Altman Z Score | Definition | exempel
- Avskrivningsformel | Exempel med Excel-mall