
Variationskoefficientformel (innehållsförteckning)
- Formel
- exempel
Vad är variationskoefficientformeln?
I statistik är variationskoefficienten som även benämns CV ett verktyg som hjälper oss att avgöra hur datapunkter i en datamängd fördelas runt medelvärdet. I princip planeras alla datapunkter först och sedan används variationskoefficienten för att mäta spridningen av dessa punkter från varandra och medelvärdet. Så det hjälper oss att förstå data och även se mönstret de bildar. Det beräknas som ett förhållande mellan standardavvikelsen för datauppsättningen till medelvärde. Högre variationskoefficient innebär att det finns en större spridning av data kring medelvärdet. På liknande sätt, sänk värdet på variationskoefficienten, desto mindre är spridningen och mer exakta blir resultaten. Även om medelvärdet för två dataserier är avsevärt olika är variationskoefficienten mycket användbar för att jämföra graden av variation från en dataserie till den andra.
Formel för variationskoefficient ges av:
Coefficient of Variation = Standard Deviation / Mean
Steg för att beräkna variationskoefficienten:
Steg 1: Beräkna medelvärdet för datauppsättningen. Medel är medelvärdet av alla värden och kan beräknas genom att ta summan av alla värden och sedan dela det med ett antal datapunkter.
Steg 2: Beräkna sedan standardavvikelsen för datauppsättningen. Det är en lite tidskrävande process. Standardavvikelse kan beräknas som: √ (Σ (X i - X m ) 2 / (n - 1)) . Xi är ith datapunkten och X m är medelvärdet för datauppsättningen. Alternativt kan vi också hitta standardavvikelsen i Excel med hjälp av STDEV.S () -funktionen.
Steg 3: Dela upp standardavvikelsen med medelvärde för att få variationskoefficienten.
Exempel på variationskoefficientformel (med Excel-mall)
Låt oss ta ett exempel för att förstå beräkningen av variationskoefficienten på ett bättre sätt.
Du kan ladda ner denna Koefficient of Variation Formula Excel Template here - Coifficient of Variation Formula Excel TemplateVariationskoefficientformel - Exempel 1
Låt oss säga att vi har två datasätt A & B och var och en innehåller 20 slumpmässiga datapunkter. Beräkna variationskoefficienten för datamängden X & Y.
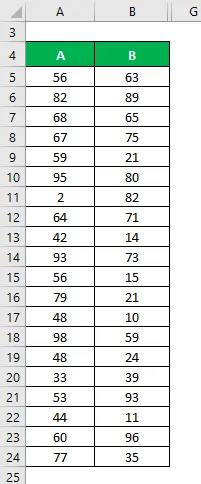
Lösning:
Medel beräknas som:
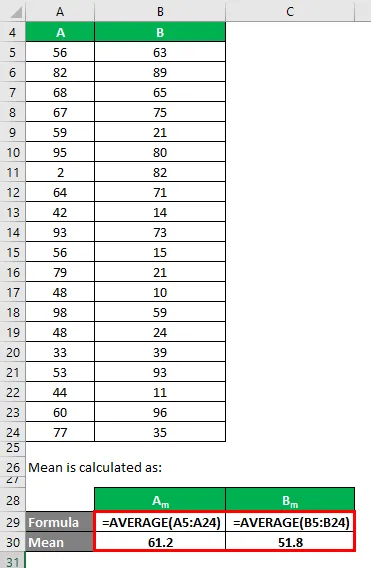
- Medeltal för datauppsättning A = 61.2
- Medeltal för datauppsättning B = 51, 8
Nu måste vi beräkna skillnaden mellan datapunkterna och medelvärdet.
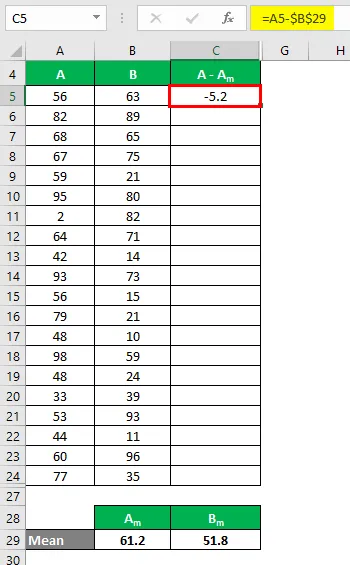
På samma sätt beräkna för alla värden i datauppsättningen A.
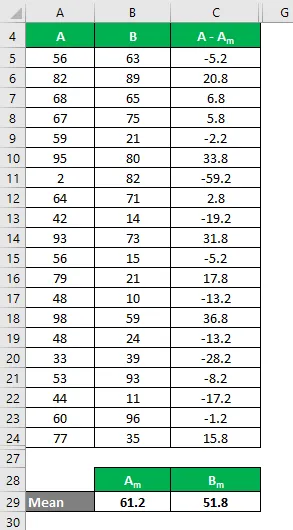
På samma sätt beräkna för alla värden i datasättet B.
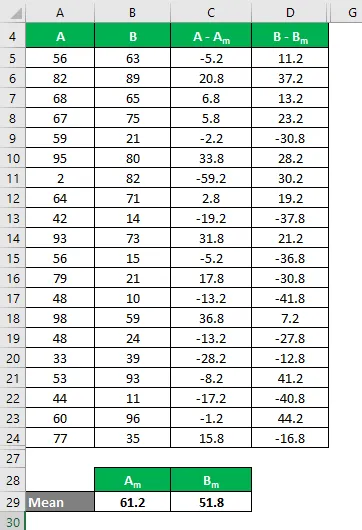
Beräkna kvadratet för skillnaden för både datamängderna A och B.
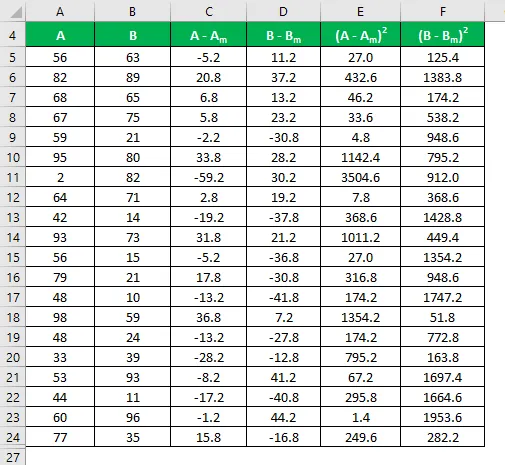
Standardavvikelse beräknas med hjälp av formeln nedan
Standardavvikelse = √ (Σ (X i - X m ) 2 / (n - 1))
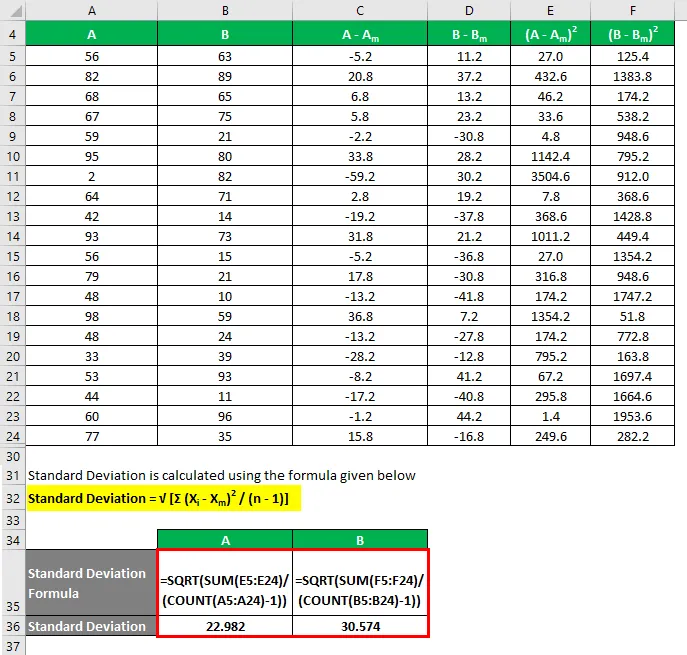
Variationskoefficient beräknas med hjälp av formeln nedan
Variationskoefficient = standardavvikelse / medelvärde
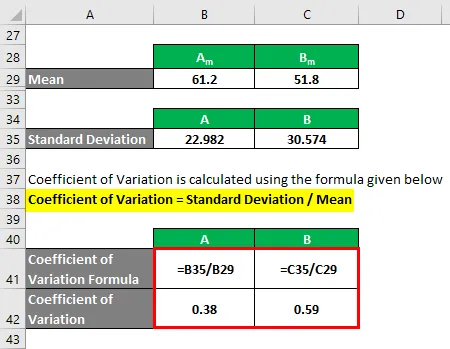
- Variationskoefficient A = 22.982 / 61.2 = 0.38
- Variationskoefficient B = 30, 574 / 51, 8 = 0, 59
Så om du ser här har B en högre variationskoefficient än A, vilket innebär att datapunkter för B är mer spridda än A.
Variationskoefficientformel - exempel # 2
Låt oss säga att du är en mycket riskvillig investerare och du vill investera pengar på aktiemarknaden. Eftersom din riskaptit är låg, vill du investera i säkra lager som har lägre standardavvikelse och variationskoefficient. Du har kortlistat 3 aktier baserat på deras grundläggande och tekniska information och vill välja två aktier. Du har också samlat information om deras historiska avkastning under de senaste 15 åren.
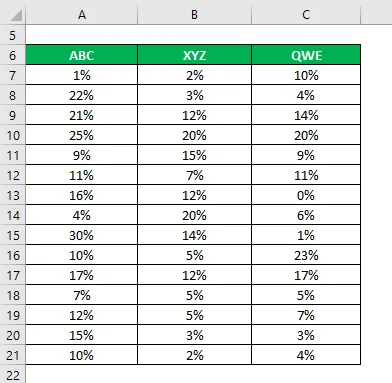
Lösning:
Medel beräknas som:
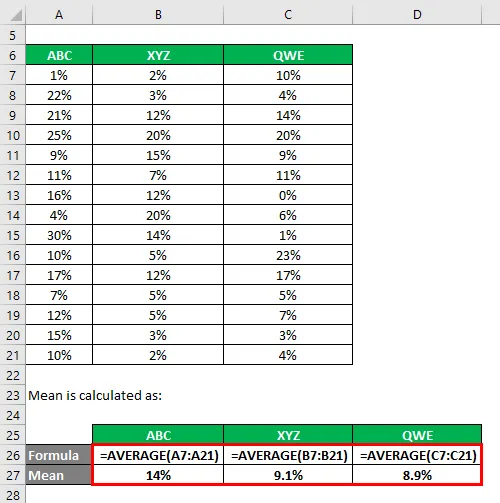
Standardavvikelse beräknas med hjälp av Excel-formel
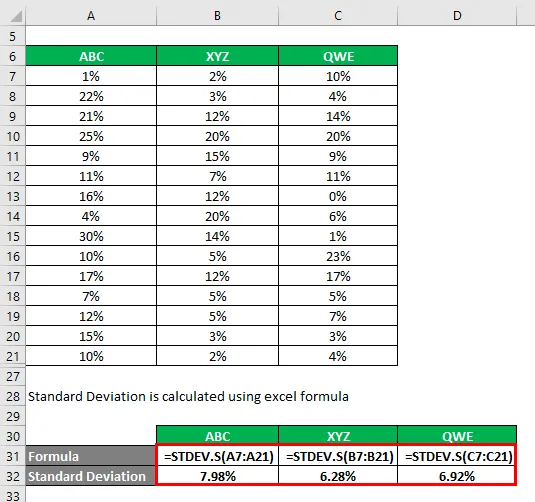
Variationskoefficient beräknas med hjälp av formeln nedan
Variationskoefficient = standardavvikelse / medelvärde
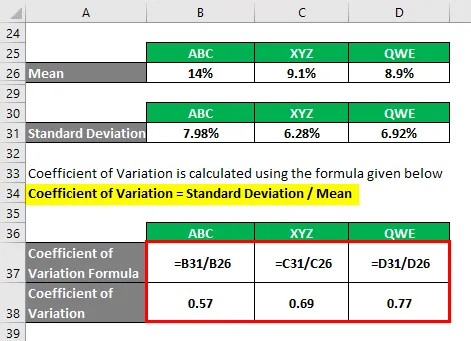
- Variationskoefficient ABC = 7, 98% / 14% = 0, 57
- Variationskoefficient XYZ = 6, 28% / 9, 1% = 0, 69
- Variationskoefficient QWE = 6, 92% / 8, 9% = 0, 77
Baserat på informationen väljer du aktie ABC och XYZ att investera eftersom de har den lägsta variationskoefficienten.
Förklaring
Eftersom variationskoefficienten är ett mått på risk hjälper det att mäta volatiliteten i priserna på aktier och andra finansiella instrument. Det hjälper också investerare och analytiker att jämföra riskerna med olika potentiella investeringar.
Variationskoefficient liknar standardavvikelse men en standardavvikelse för två variabler kan inte jämföras i användbarhet. Men att använda standardavvikelse och medelvärdet gör den relativa jämförelsen mer meningsfull. Det finns en begränsning av variationskoefficienten också. Anta att medelvärdet för en datamängd är noll. I så fall kommer detta verktyg att bli ineffektivt. Inte bara detta, om vi har en datauppsättning som har många positiva och negativa värden, blir variationskoefficienten mycket problematisk. Så det är bara mer användbart med datauppsättningar med samma plus-minus-tecken.
Relevans och användningsformer för variationskoefficient
Variationskoefficient har relevans inom många andra områden än statistik. Till exempel inom finansområdet är variationskoefficienten ett mått på risk. Det liknar standardavvikelse eftersom det också används som ett mått på risk men skillnaden är att variationskoefficienten är en bättre indikator på relativ risk. Låt oss till exempel säga A: s förväntade avkastning på 15% och B: s förväntade avkastning på 10% och A har en standardavvikelse på 10%, medan B har en standardavvikelse på 5%. För att välja en bättre investering kan variationskoefficienten användas. Så variationskoefficienten för A är 10/15 = 0, 666 och variationskoefficienten för B är 5/10 = 0, 5. Så B är en bättre investering än A.
Rekommenderade artiklar
Detta har varit en guide till Formel för variationskoefficient. Här diskuterar vi hur man beräknar variationskoefficienten med hjälp av formel tillsammans med praktiska exempel och nedladdningsbar Excel-mall. Du kan också titta på följande artiklar för att lära dig mer -
- Vad är justerad R-kvadratformel?
- Exempel på bestämningskoefficientformel
- Hur man beräknar korrelationskoefficient med formel?
- Covariance-formel med Excel-mall