Komplexa nummer i MATLAB - Hur man genererar komplexa nummer?

Introduktion till komplexa nummer i MATLAB

Komplexa siffror är en kombination av verkliga siffror och imaginära nummer i form av p + qi där p och q är de verkliga siffrorna och i är det imaginära talet. Ett imaginärt tal definieras där i är resultatet av en ekvation a 2 = -1. Vi kan använda i eller j för att beteckna de imaginära enheterna. Eftersom komplexa nummer används i alla matematiska beräkningar och Matlab används främst för att utföra matematiska beräkningar. Så komplexa nummer utgör en viktig del av att lära sig Matlab.

Generering av komplexa nummer i MATLAB

Komplexa nummer kan skapas eller deklareras i Matlab med hjälp av en "komplex" funktion. Vi kan också skapa komplexa siffror genom att hitta kvadratroten till vilket negativt tal som helst. I Matlab kan vi använda i eller j för att beteckna den imaginära delen av det komplexa antalet.

exempel

X = 4 + 5i

Här är X ett komplext nummer som innehåller 2 delar, dvs verklig och imaginär del. 4 är den verkliga delen och 5 är den imaginära delen. Vi kan hitta de verkliga och imaginära delarna med hjälp av funktioner i Matlab.

a = real (X) = 4 (Detta ger den verkliga delen av det komplexa antalet)
b = imag (X) = 5 (Detta ger den imaginära delen av det komplexa antalet)
komplex (6, 7) = 6 + 7i (Den här funktionen används för att skapa komplexa tal)

Vi kan också skapa komplexa matriser i Matlab som också kan deklareras med komplexa funktioner.

a = komplex (x, y)

Det finns vissa villkor för x och y som vi bör följa som x och y bör inte vara enkla eller dubbla. En komplex skalar kan skapas om två ingångar är skalära i naturen,

X = komplex (5, 3)
X = 5, 0000 + 3, 0000i

På liknande sätt kan en komplex vektor skapas om vi har två ingångar som vektorer.

X = uint8 ((4; 5; 6; 7));
Y = uint8 ((3; 5; 1; 2));
a = komplex (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Vi kan skapa ett komplext nummer som bara har en skalar som,

X = komplex (10)
X = 10, 0000 + 0, 0000i

Det finns vissa förhållanden som inmatnings- och utgångsargumenten bör följa,

Inmatningsargumenten innehåller verkliga och imaginära delar som x valfri y. x och y ska vara skalar, vektor, flerdimensionell matris eller matris i MATLAB. Storleken på x och y ska vara densamma. De bör vara av samma datatyp men det finns få undantag som dubbla kan användas med enstaka och heltal kan kombineras med en dubbel som är skalär.

Utmatningen från matrisen kan vara vektor-, skal-, matris- eller flerdimensionell matris beroende på ingångsargumenten. Storleken på utgången ska vara densamma som ingången. Om ingångsargumenten har olika datatyper än utgången bestäms av,

Om någon av ingångsargumenten har en enda karaktär, bör utgången också vara singel.
Om någon av ingångsargumenten har ett heltal till sin natur, bör utgången vara av ett heltaldatatyp.

Vi kan kontrollera om matrisen är verklig eller imaginär genom att använda isreal funktion.

Koda:

X = (2+i, 1); Isreal(X)

Produktion:

Koda:

Isreal (X (2))

Produktion:

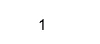
För att extrahera de verkliga och imaginära delarna kan vi använda riktiga och imagefunktioner i Matlab som,

Koda:

real(X)

Produktion:

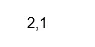
Koda:

imag(X)

Produktion:

Operationer och funktioner för komplexa nummer i MATLAB

Det finns flera operationer och funktioner som kan utföras med komplexa nummer i Matlab som

abs: Den här funktionen används för att hitta modulen för alla komplexa nummer i form av p + qi. abs (2 + 3i) = kvadratrot av (2 2 + 3 2) = (13) 0, 5
vinkel: För att hitta fasvinkeln för det komplexa talet.

Det finns vissa tips som bör följas för att komplexa tal i Matlab ska fungera korrekt,

Vi bör undvika att använda i och j som en del av alla variabla namn eftersom de används för att beteckna de imaginära delarna av det komplexa numret.
Vi bör undvika att använda j eller i om den imaginära delen är 1. Istället kan vi använda 1j eller 1i.
Vi kan skapa en komplex funktion i Matlab när i och j används som variabla namn i någon del, ingångsargument är inte av enstaka eller dubbel typ och den imaginära delen är noll.

Slutsats

Komplexa nummer används inom det matematiska eller tekniska området. Många verkliga eller praktiska tillämpningar kan beskrivas med hjälp av den imaginära delen av komplexa nummer. Så att förstå användningen och tillämpningarna av komplexa nummer i olika plattformar är viktigt, särskilt om du har att göra med någon fysisk eller matematisk domän.

Rekommenderade artiklar

Detta är en guide till komplexa nummer i MATLAB. Här diskuterar vi introduktionen och komplexa talgenerering i matlab inklusive dess exempel med funktion och funktion. Du kan också titta på följande artiklar för att lära dig mer-