
Bestämningskoefficientformel (innehållsförteckning)
- Formel
- exempel
Vad är bestämningskoefficienten för bestämning?
I statistik är bestämningskoefficient, även benämnd R 2 ett verktyg som bestämmer och bedömer förmågan hos en statistisk modell att förklara och förutsäga framtida resultat. Med andra ord, om vi har beroende variabel y och oberoende variabel x i en modell, hjälper R 2 att bestämma variationen i y med variation x. Det är en av de viktigaste utgångarna från regressionsanalys och används när vi vill förutsäga framtida eller testa vissa modeller med relaterad information. Värdet på R 2 ligger mellan 0 och 1 och högre R2-värdet, bättre blir modellens förutsägelse och styrka. R2 är mycket lik korrelationskoefficienten eftersom korrelationskoefficienten mäter den direkta sammanslutningen av två variabler. R2 är i princip en kvadrat av en korrelationskoefficient.
Formel för bestämningskoefficient:
Det finns flera formler för att beräkna bestämningskoefficienten:
- Använda korrelationskoefficient:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Var:
- X - Datapunkter i datauppsättning X
- Y - Datapunkter i datauppsättningen Y
- X m - Medeltal för datauppsättning X
- Y m - Medeltal för datamängden Y
Så
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Använda regressionsutgångar
Bestämningskoefficient (R2) = förklarad variation / total variation
Bestämningskoefficient (R2) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Var:
- TSS - Total summa av kvadrater = Σ (Yi - Ym) 2
- MSS - Model Sum of Squares = Σ (Y - Ym) 2
- RSS - Rest summa av kvadrater = Σ (Yi - Y ^) 2
Y är modellens förutspådda värde, Yi är ith-värdet och Ym är medelvärdet
Exempel på formel för bestämningskoefficient (med Excel-mall)
Låt oss ta ett exempel för att förstå beräkningen av bestämningskoefficienten på ett bättre sätt.
Du kan ladda ner denna bestämningskoefficientformulär Excel-mall här - Bestämningskoefficientformulär Excel-mallBestämningskoefficientformel - Exempel 1
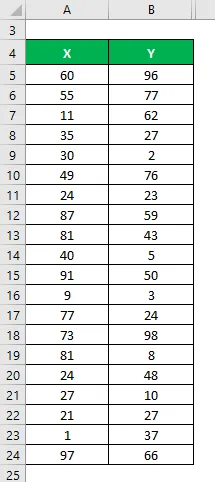
Låt oss säga att vi har två datauppsättningar X & Y och var och en innehåller 20 slumpmässiga datapunkter. Beräkna bestämningskoefficienten för datamängden X & Y.
Medel beräknas som:
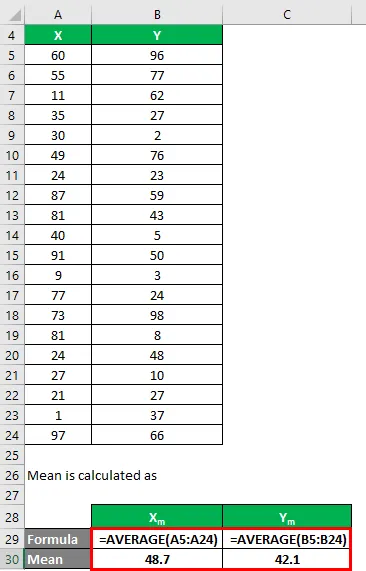
- Genomsnitt för datauppsättning X = 48, 7
- Medeltal för datamängden Y = 42.1
Nu måste vi beräkna skillnaden mellan datapunkterna och medelvärdet.
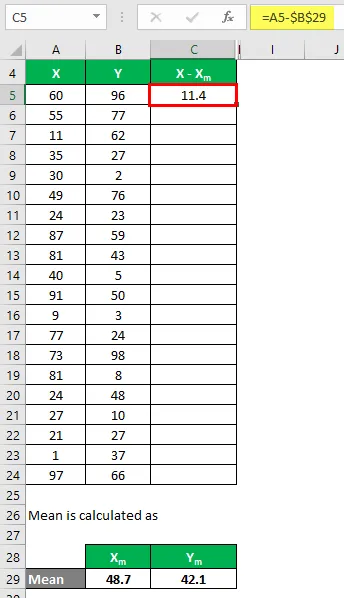
På samma sätt beräkna för all datauppsättning av X.
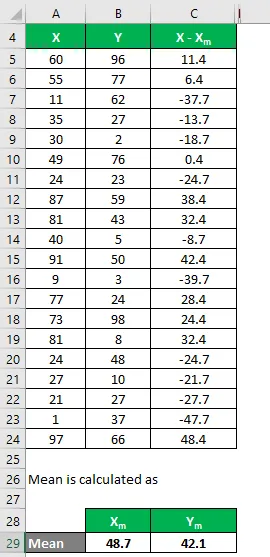
På samma sätt kan du också beräkna det för datamängden Y.

Beräkna kvadratet för skillnaden för både datamängderna X och Y.
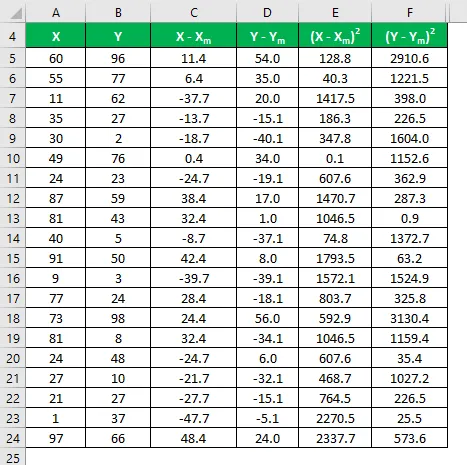
Multiplicera skillnaden i X med Y.
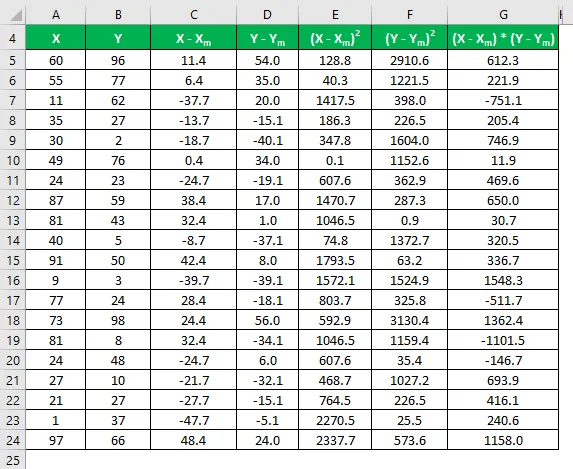
Korrelationskoefficient beräknas med hjälp av formeln nedan
Korrelationskoefficient = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
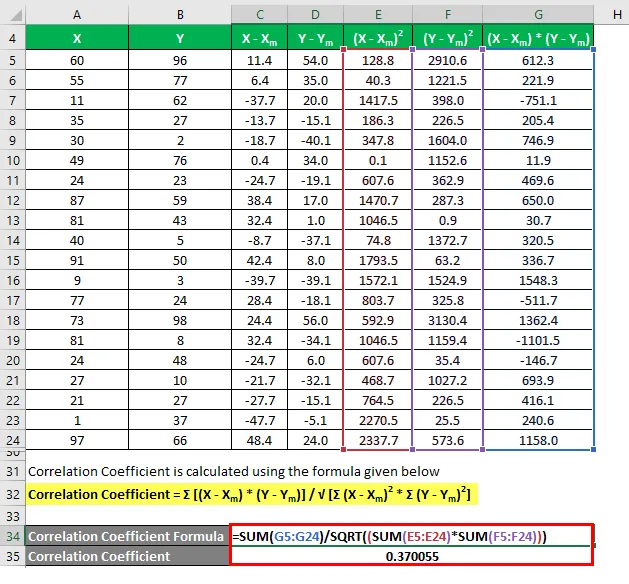
Bestämningskoefficient beräknas med hjälp av formeln nedan
Bestämningskoefficient = (korrelationskoefficient) 2
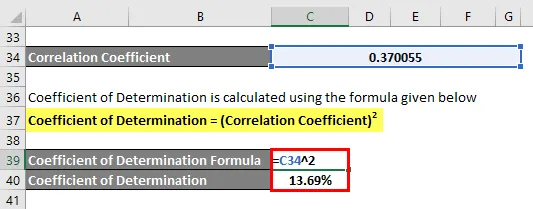
Bestämningskoefficient = 13, 69%
Bestämningskoefficientformel - exempel # 2
Låt oss säga att du är en mycket riskvillig investerare och du vill investera pengar på aktiemarknaden. Du är inte säker på vilka aktier du ska investera i och din riskaptit är låg. Så du vill investera i en aktie som är säker och som kan efterlikna indexets prestanda. Din vän, som är en aktiv investerare, har kortlistat 3 aktier åt dig baserat på deras grundläggande och tekniska information och du vill välja två aktier bland dessa tre.
Du har också samlat information om deras historiska avkastning under de senaste 15 åren.
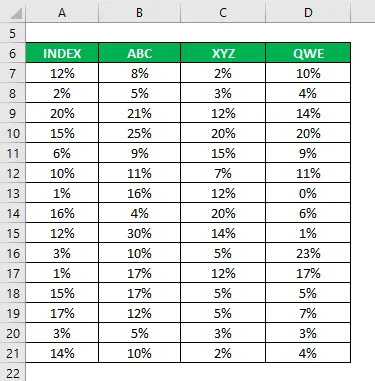
Korrelationskoefficient beräknas med hjälp av excel-formeln
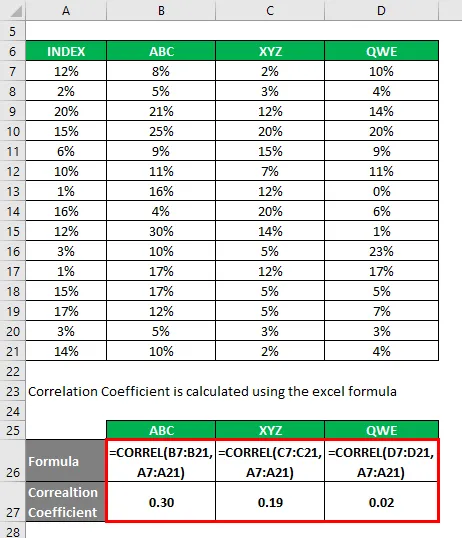
Bestämningskoefficient beräknas med hjälp av formeln nedan
Bestämningskoefficient = (korrelationskoefficient) 2
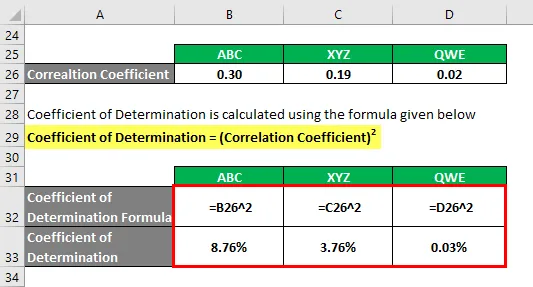
Baserat på informationen kommer du att välja aktie ABC och XYZ att investera eftersom de har den högsta bestämningskoefficienten.
Förklaring
Såsom förklarats ovan är bestämningskoefficienten kvadratet för korrelationen mellan två datamängder. Om R2 är 0 betyder det att det inte finns någon korrelation och oberoende variabel kan inte förutsäga värdet på den beroende variabeln. På samma sätt, om dess värde är 1, betyder det att oberoende variabel alltid kommer att lyckas med att förutsäga den beroende variabeln. Men det finns vissa begränsningar också. Även om det berättar om sambandet mellan två datasätt, berättar det inte för oss om det värdet är tillräckligt eller inte.
Dessutom innebär stort värde R2 inte alltid att de två variablerna har starka förhållanden och det kan vara en fluke. Till exempel: Låt oss säga R 2- värde mellan ett antal bilar som sålts under ett år och antalet glassförpackningar som sålts under ett år är 80%. Men det finns inget samband mellan dessa två. Så man bör vara mycket försiktig när man använder R 2 och först förstå data och sedan använda metoden
Relevans och användningsformer för bestämningskoefficient
Det finns många praktiska tillämpningar av R 2 . Till exempel används R2 vanligtvis av investerare för att jämföra deras portföljs prestanda med marknaden och försöka förutsäga framtida riktningar. På liknande sätt hjälper hedgefonder R 2 att modellera risken i sina modeller. Men slutligen är resultatet baserat på rena siffror och statistik som ibland kan vara vilseledande. Som nämnts ovan måste man först kontrollera om utgången från R 2 är vettig i verkligheten eller inte.
Rekommenderade artiklar
Detta har varit en guide till formel för bestämningskoefficient. Här diskuterar vi hur man beräknar bestämningskoefficienten tillsammans med praktiska exempel och nedladdningsbar Excel-mall. Du kan också titta på följande artiklar för att lära dig mer -
- Guide till formel för marknadsriskpremie
- Exempel på formel för täckningsgrad
- Kalkylator för aktivitetsbaserad kostnadsformel
- Hur man beräknar informationsförhållande med formel?