
Introduktion till funktioner i R
Funktionen definieras som en uppsättning uttalanden, för att utföra och utföra alla specifika logiska uppgifter. Funktionen tar några inmatningsparametrar som kallas argument för att utföra denna uppgift. Funktioner hjälper till att bryta koden, till enklare bitar genom att orkestrera den logiskt, vilket är lättare att läsa och förstå. I det här ämnet kommer vi att lära oss om funktioner i R.
Hur man skriver funktioner i R?
För att skriva funktionen i R är här syntaxen:
Fun_name <- function (argument) (
Function body
)
Här kan man se "funktions" specifikt reserverat ord används i R för att definiera vilken funktion som helst. Funktionen tar input som är i form av argument. Funktionsorganet är en uppsättning logiska uttalanden som utförs över argument och sedan returnerar den utdata. "Fun_name" är det namn som ges till funktionen, genom vilken den kan kallas var som helst i R-programmet.
Låt oss se ett exempel som kommer att vara mer klar när vi förstår funktionen i R.
R-kod
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
produktion:
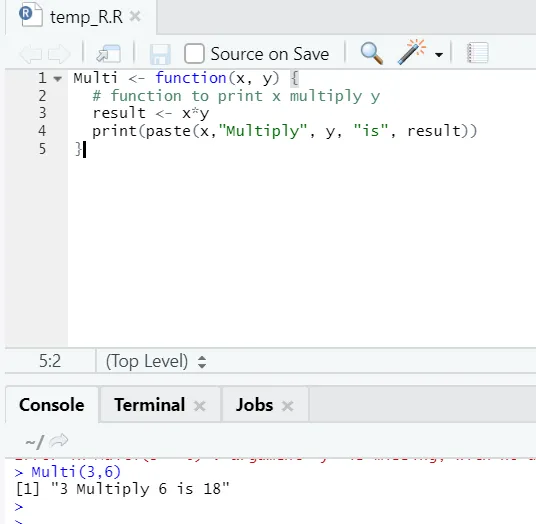
Här skapade vi funktionsnamnet "Multi", som tar två argument som ingångar och ger den multiplicerade utgången. Det första argumentet är x och det andra argumentet är y. Som ni ser har vi kallat funktionen under namnet “Multi”. Om någon vill här kan argument också ställas in på standardvärdet.
Olika typer av funktioner i R
Olika R-funktioner med syntax och exempel (inbyggd, matematik, statistik, etc.)
1) Inbyggd funktion -
Dessa är de funktioner som följer med R för att adressera en specifik uppgift genom att ta ett argument som input och ge en utgång baserad på den givna ingången. Låt oss diskutera några viktiga allmänna funktioner för R här:
a) Sortera: Data kan vara av typen till stigande eller fallande ordning. Data kan vara huruvida en vektor med fortsättningsvariabel eller faktorvariabel.
Syntax:

Här är förklaringen av dess parametrar:
- x: Detta är en vektor för den kontinuerliga variabeln eller faktorvariabeln
- minskar: Detta kan ställas in antingen Sann / Falsk för att styra ordningen genom att stiga eller sänka. Som standard är det FALSE`.
- sista: Om vektorn har NA-värden, ska den läggas senast eller inte
R-kod och utgång:
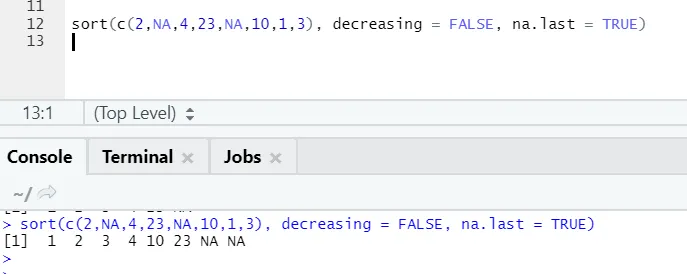
Här kan man lägga märke till hur ”NA” -värden justeras i slutet. Som vår parameter na.last = True var sant.
b) Sekvens: Den genererar en sekvens av numret mellan två specificerade nummer.
Syntax
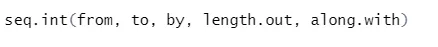
Här är förklaringen av dess parametrar:
- från, till start- och slutvärdet för sekvensen.
- av: Ökning / gap mellan två på varandra följande nummer i följd
- length.out: den erforderliga längden på sekvensen.
- Along.with: Avser längden från argumentets längd
R-kod och utgång:
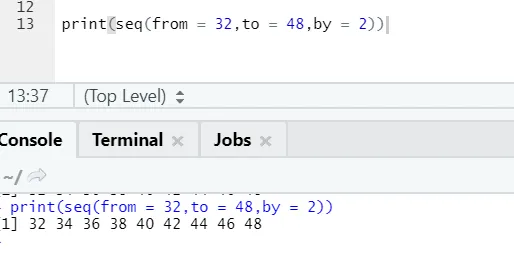
Här kan man märka att den sekvens som genereras har en inkrementering av 2 eftersom by definieras som 2.
c) Toupper, tolower: De två funktionerna: toupper och tolower är funktioner som används på strängen för att ändra bokstäverna i meningar.
R-kod och utgång:
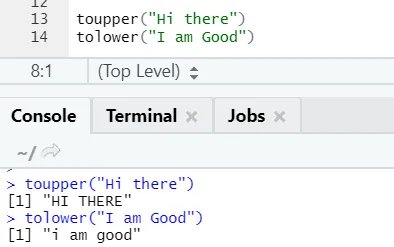
Man kan se hur bokstäverna ändras när de tillämpas på funktionen.
d) Rnorm: Detta är en inbyggd funktion som genererar slumpmässiga nummer.
R-kod och utgång:
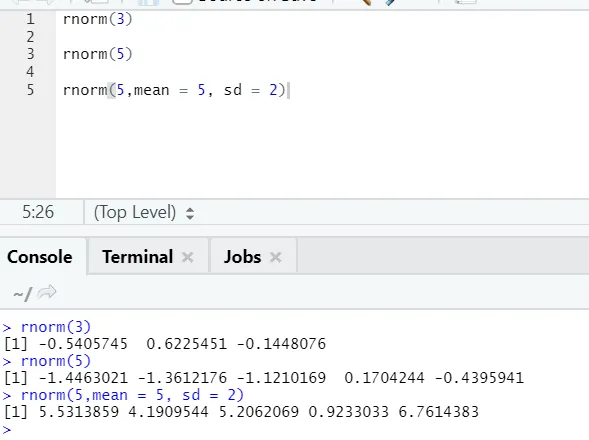
Funktionen rnorm tar det första argumentet som säger hur många siffror som behöver genereras.
e) Rep: Denna funktion replikerar värdet så många gånger som anges.
R-syntax: rnorm (x, n)
Här representerar x värde för att replikera, och n representerar antalet gånger det måste replikeras.
R-kod och utgång:
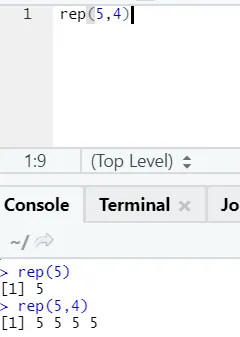
f) Klistra in: Denna funktion är att sammanfoga strängar tillsammans med någon specifik karaktär däremellan.
syntax
paste(x, sep = “”, collapse = NULL)
R-kod
paste("fish", "water", sep=" - ")
R-utgång:
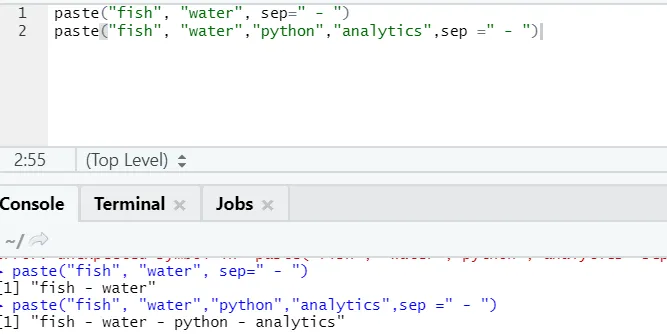
Som ni ser kan vi klistra in mer än två strängar också. Sep är den specifika karaktären som vi lagt till mellan strängarna. Som standard är sep utrymme.
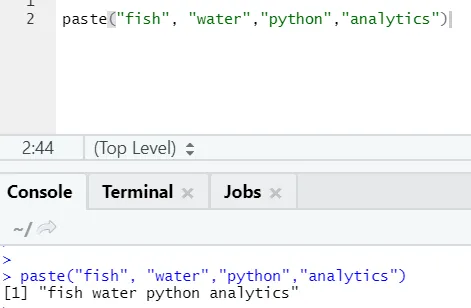
En liknande funktion finns som denna, som alla bör vara medvetna om är paste0.
Funktionspasta0 (x, y, kollaps) fungerar som att klistra in (x, y, sep = “”, kollaps)
Se exemplet nedan:
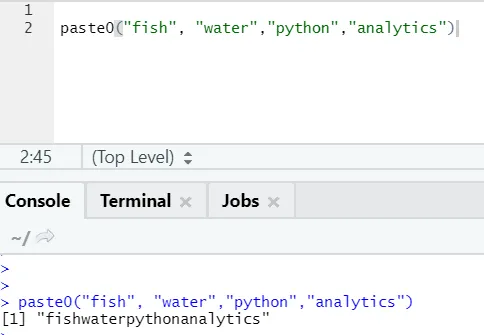
Med enkla ord för att sammanfatta klistra in och klistra0:
Klistra in0 är snabbare än klistra in när det gäller sammankopplingen av strängar utan någon separator. Eftersom klistra alltid letar efter “sep” och som är utrymme som standard i det.
g) Strsplit: Denna funktion är att dela strängen. Låt oss se de enkla fallen:
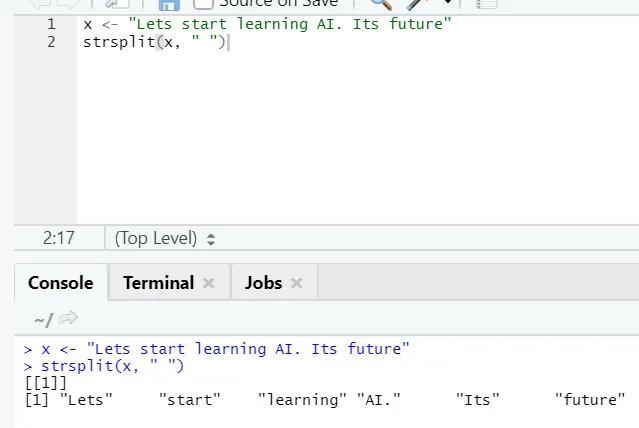
h) Rbind: Funktionen rbind hjälper till att kombinera vektorer med samma antal kolumner, en över varandra.
Exempel
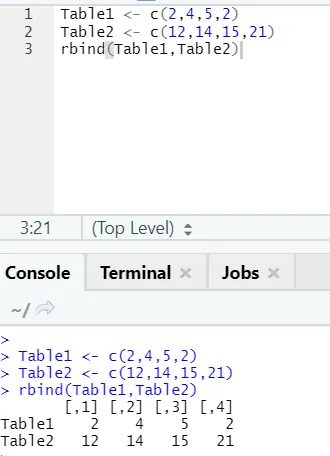
i) cbind: Detta kombinerar vektorer med samma antal rader, sida vid sida.
Exempel
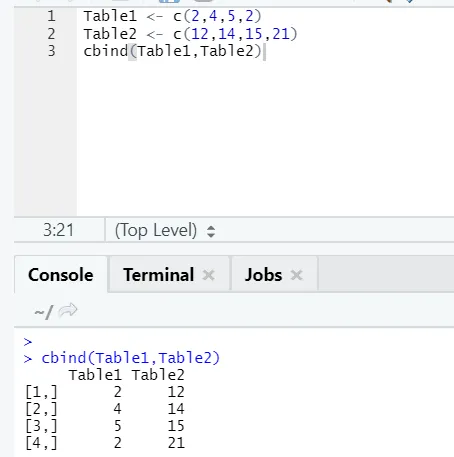
Om antalet rader inte stämmer överens är felet nedan:

Både cbind och rbind hjälper till att manipulera och omforma.
2) Matematikfunktion -
R tillhandahåller en mängd olika matematikfunktioner. Låt oss se några av dem i detalj:
a) Sqrt: Denna funktion beräknar kvadratroten för ett nummer eller en numerisk vektor.
R-kod och utgång:
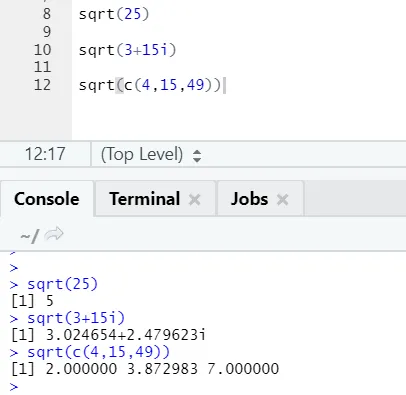
Man kan se hur kvadratroten av ett nummer, ett komplext antal och en sekvens av numerisk vektor har beräknats.
b) Exp: Denna funktion beräknar det exponentiella värdet för ett nummer eller en numerisk vektor.
R-kod och utgång:
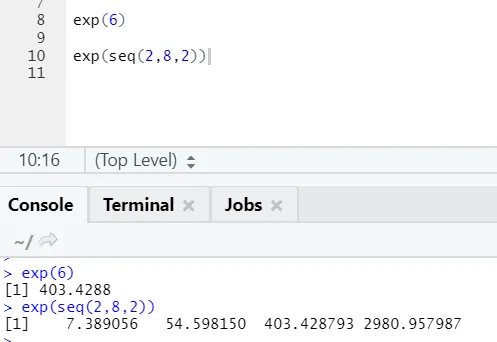
c) Cos, Sin, Tan: Dessa är trigonometrifunktioner implementerade i R här.
R-kod och utgång:
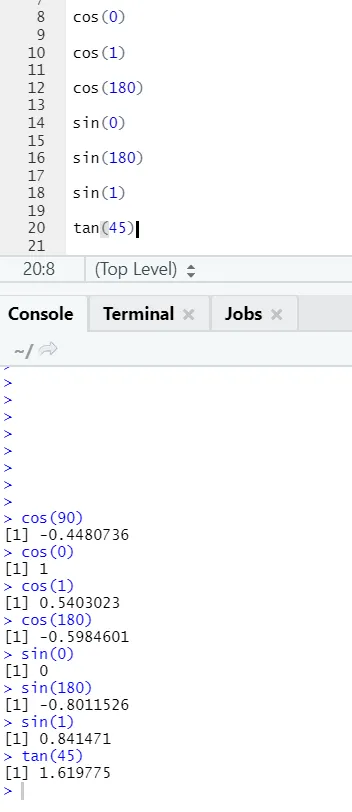
d) Abs: Denna funktion returnerar det absoluta positiva värdet för ett nummer.
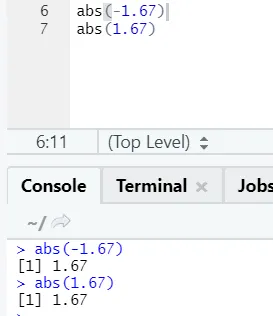
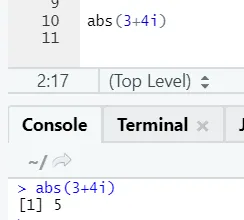
Som ni ser kommer det negativa eller positiva av ett nummer att returneras i dess absoluta form. Låt oss se det för ett komplext nummer:
e) Logg: Detta är för att hitta logaritmen för ett nummer.
Här är exemplet som visas nedan:
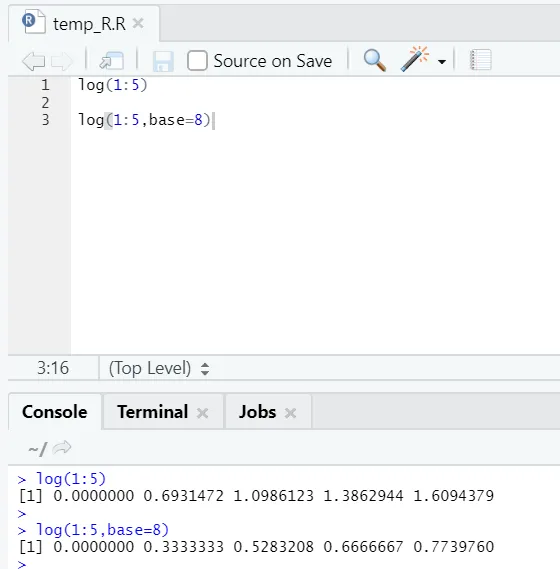
Här får man flexibiliteten att byta bas enligt krav.
f) Cumsum: Detta är en matematisk funktion som ger kumulativa summor. Här är exemplet nedan:
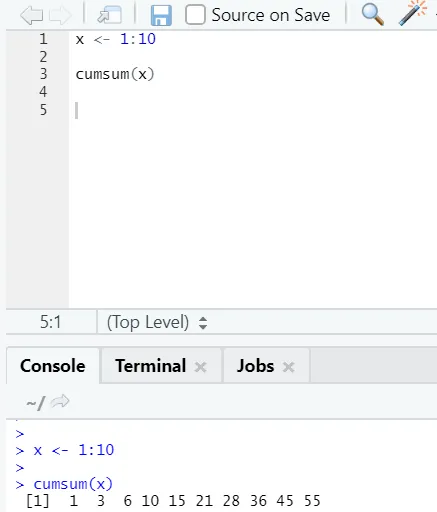
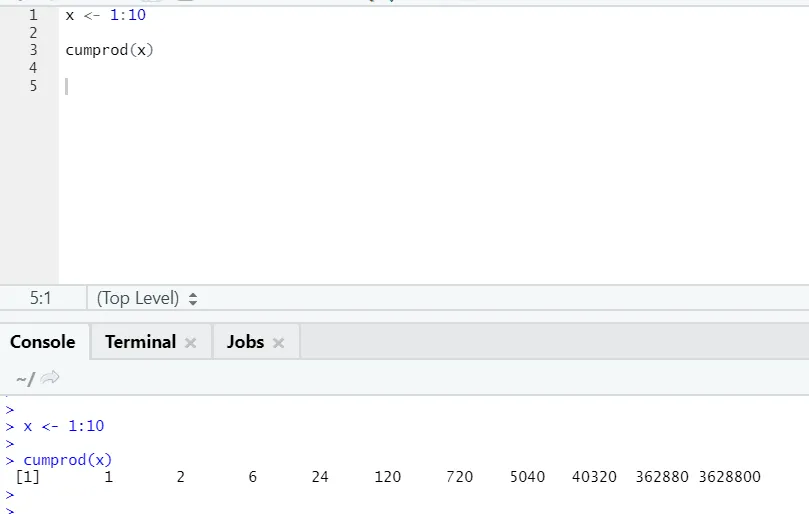
g) Cumprod: Liksom matematisk Cumsum-funktion har vi cumprod där kumulativ multiplikation sker.
Se exemplet nedan:
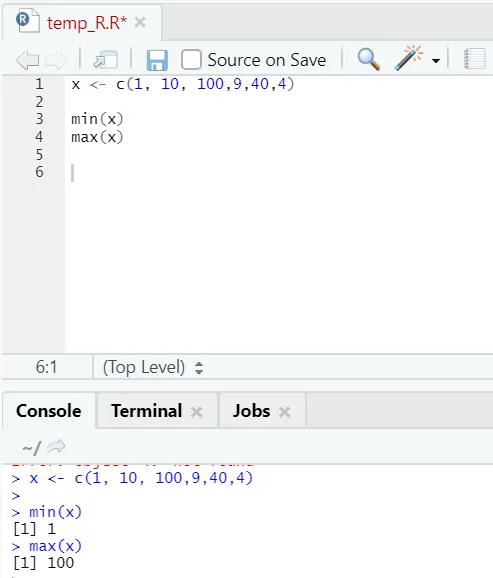
h) Max, Min: Detta hjälper dig att hitta det maximala / minsta värdet i uppsättningen av siffror. Se nedan exempel relaterade till detta:
i) Tak: Taket är en matematisk funktion som returnerar det minsta av heltalet högre än specificerat.
Låt titta på ett exempel:
tak (2, 67)
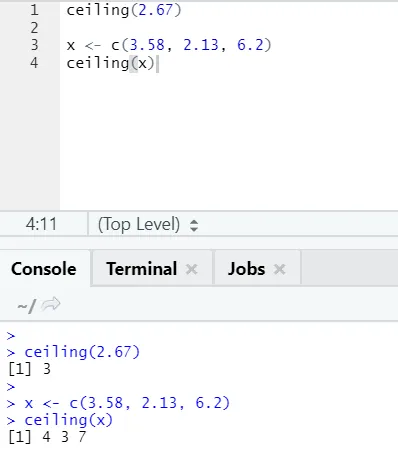
Som ni kan märka appliceras taket på såväl ett antal som över en lista, och utmatningen kom är den minsta av nästa högre heltal.
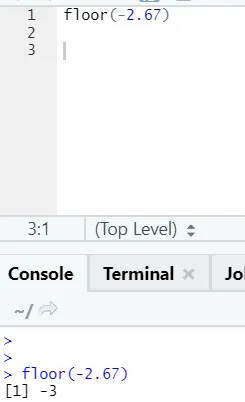
j) Golv: Golvet är en matematisk funktion som ger det minsta värdet heltal för det angivna antalet.
Exemplet nedan hjälper dig att förstå det bättre:
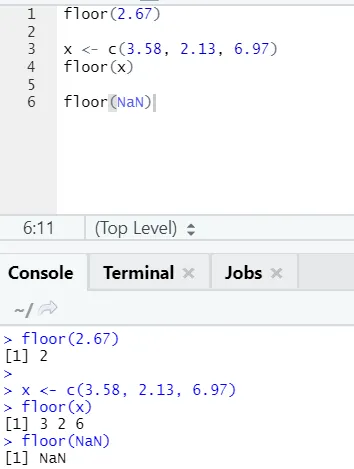
Det fungerar på samma sätt även för negativa värden. Ta en titt:
3) Statistiska funktioner -
Dessa är de funktioner som beskriver den relaterade sannolikhetsfördelningen.
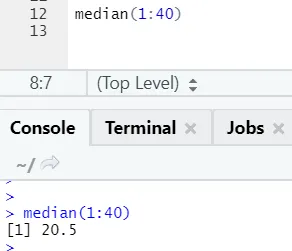
a) Median: Detta beräknade median utifrån nummersekvensen.
Syntax
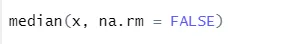
R-kod och utgång:
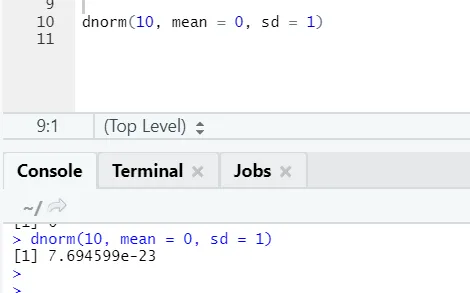
b) Dnorm: Detta avser normalfördelningen. Funktionen dnorm returnerar värdet för sannolikhetsdensitetsfunktionen för den normala fördelningen som ges parametrar för x, μ och σ.
R-kod och utgång:
c) Cov: Covariance berättar om två vektorer är positivt, negativt eller helt oberoende.
R-kod
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
R-utgång:
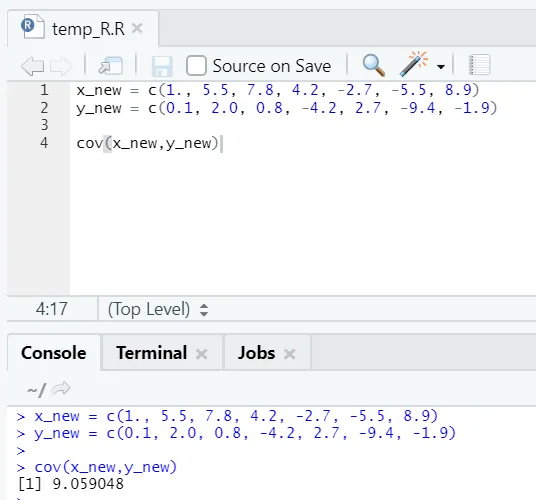
Som ni ser är två vektorer positivt relaterade, vilket innebär att båda vektorerna rör sig i samma riktning. Om samvariationen är negativ betyder det att x och y är omvänt relaterade och därmed rör sig i motsatt riktning.
d) Cor: Detta är en funktion för att hitta sambandet mellan vektorer. Det ger faktiskt associeringsfaktorn mellan de två vektorerna som kallas ”korrelationskoefficienten”. Korrelation lägger till en gradfaktor över kovarians. Om två vektorer är positivt korrelerade, kommer korrelationen också att säga dig med hur mycket förlängning de är positivt relaterade.
Dessa tre typer av metoder som kan användas för att hitta en korrelation mellan två vektorer:
- Pearson korrelation
- Kendall korrelation
- Spearman-korrelation
I enkelt R-format ser det ut som:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Här är x och y vektorer.
Låt oss se det praktiska exemplet på korrelation mellan ett inbyggt datasätt.
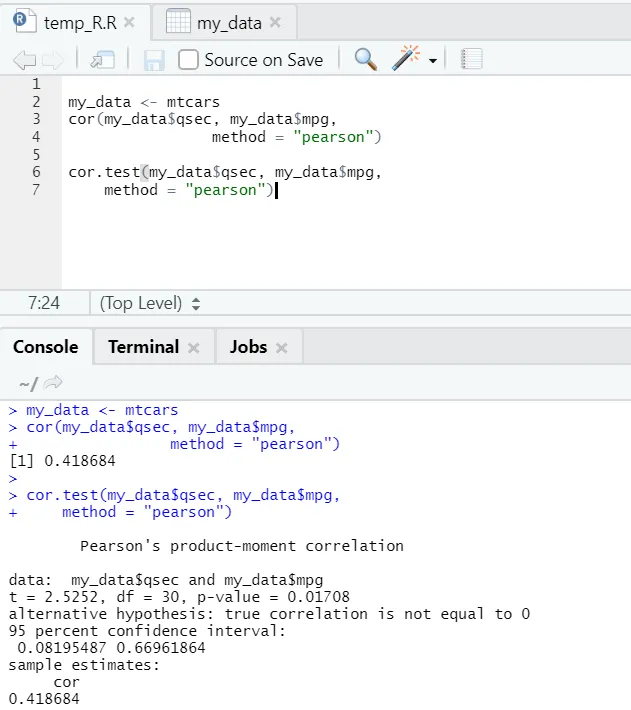
Så här kan du se funktionen "cor ()" gav korrelationskoefficienten 0, 41 mellan "qsec" och "mpg". Emellertid har ytterligare en funktion visats fram, dvs "cor.test ()", som inte bara berättar korrelationskoefficienten utan också p-värdet och t-värdet relaterat till det. Tolkning blir mycket enklare med cor.test-funktion.
Liknande kan göras med de andra två metoderna för korrelation:
R-kod för Pearson-metoden:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
R-kod för Kendall-metoden:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
R-kod för Spearman-metoden:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
Korrelationskoefficienten sträcker sig mellan -1 och 1.
Om korrelationskoefficienten är negativ, innebär det att x ökar y minskar.
Om korrelationskoefficienten är noll, innebär det att det inte finns någon associering mellan x och y.
Om korrelationskoefficienten är positiv, innebär det att när x ökar y tenderar det också att öka.
e) T-test: T-testet kommer att berätta om två datauppsättningar kommer från samma (förutsatt) normala fördelningar eller inte.
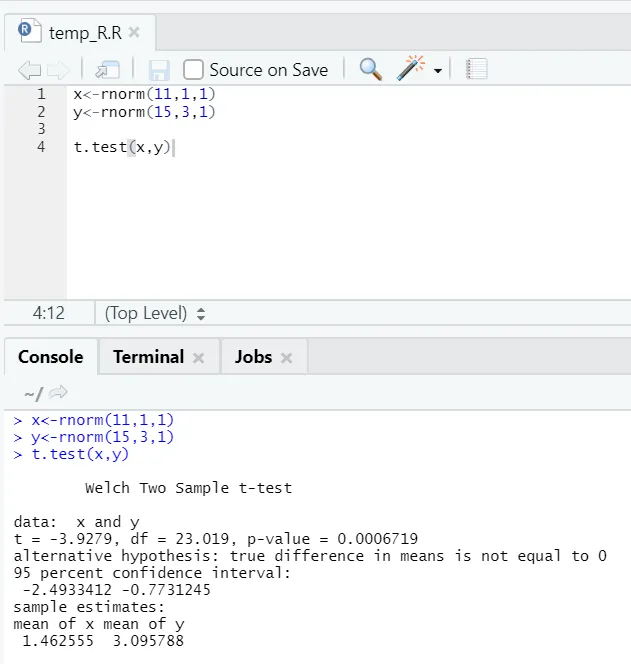
Här bör du avvisa nollhypotesen att de två medlen är lika eftersom p-värdet är mindre än 0, 05.
Den här visade instansen är av typ: oparade datauppsättningar med ojämlika variationer. På liknande sätt kan du prova med det parade datasättet.
f) Enkel linjär regression: Detta visar förhållandet mellan prediktorn / oberoende och respons / beroende variabel.
Ett enkelt praktiskt exempel kan vara att förutsäga en persons vikt om höjden är känd.
R syntax
lm(formula, data)
Här visar formeln förhållandet mellan output dvs. y och ingångsvariabel iex Data representerar datasättet, på vilket formeln måste tillämpas.
Låt oss se ett praktiskt exempel, där golvytan är ingångsvariabeln och hyra är utgångsvariabeln.
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
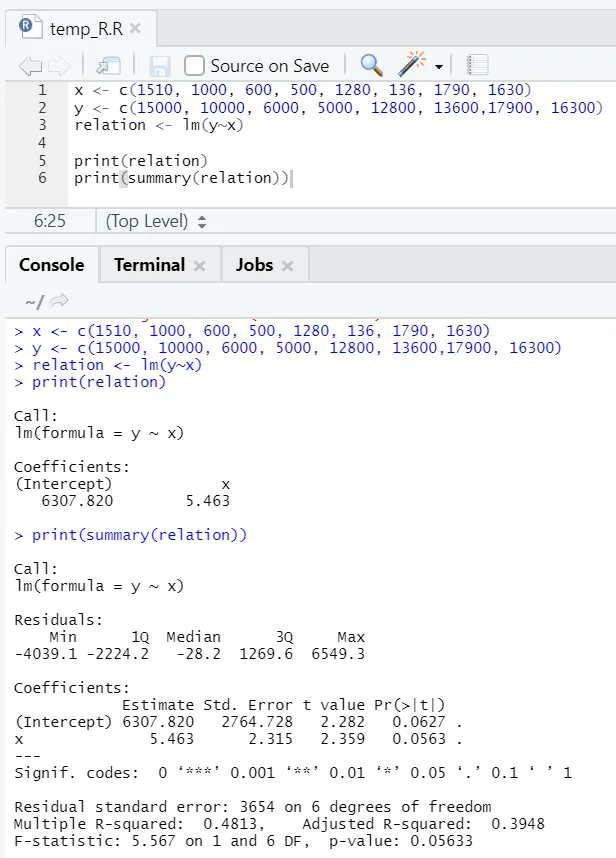
Här är P-värdet inte mindre än 5%. Därför kan nollhypotesen inte avvisas. Det är inte mycket viktigt att bevisa förhållandet mellan golvytan och hyran.
Här är R-kvadratvärdet 0, 4813. Det innebär att endast 48% av variansen i utmatningsvariabeln kan förklaras av inmatningsvariabeln.
Låt oss säga att nu måste vi förutse ett värde på golvyta, baserat på den ovan monterade modellen.
R-kod
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
R-utgång:
Efter exekveringen av ovanstående R-kod ser utdata ut enligt följande:
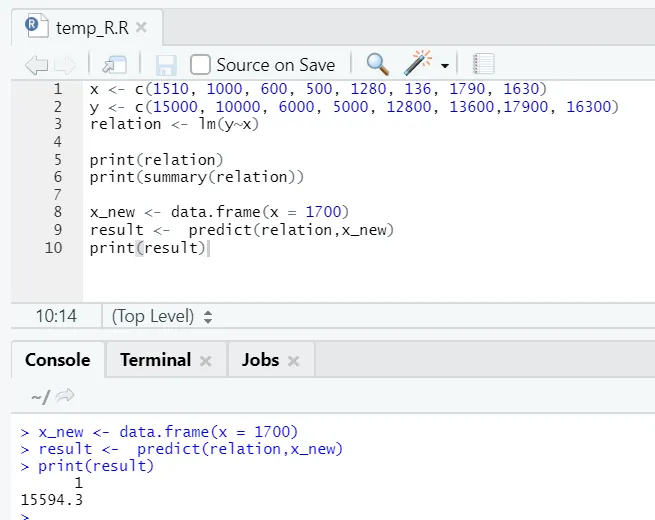
Man kan passa och visualisera regression. Här är R-koden för det:
# Ge png-diagramfilen ett namn.
png(file = "LinearRegressionSample.png.webp")
# Plotta diagrammet.
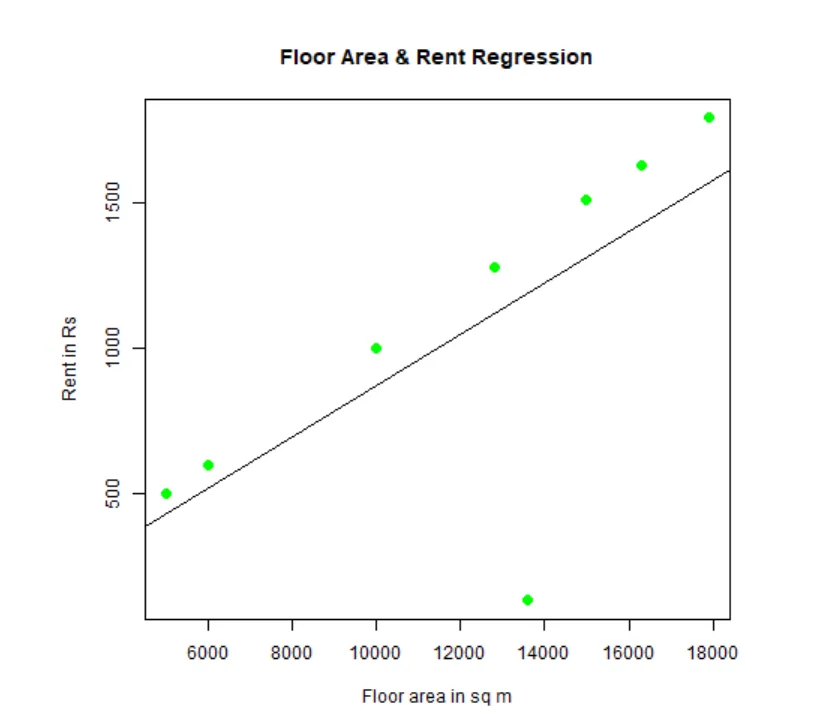
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Spara filen.
dev.off()
Den här linjen "LinearRegressionSample.png.webp" kommer att genereras i din nuvarande arbetskatalog.
g) Chi-Square-test
Detta är en statistisk funktion i R. Detta test har sin betydelse för att bevisa om korrelationen finns mellan två kategoriska variabler.
Detta test fungerar också som alla andra statistiska test baserade på p-värde, man kan acceptera eller avvisa nollhypotesen.
R syntax
chisq.test(data), /code>
Låt oss se ett praktiskt exempel på det.
R-kod
# Ladda biblioteket.
library(datasets)
data(iris)
# Skapa en dataram från huvuduppsättningen.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Skapa en tabell med nödvändiga variabler.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Utför Chi-Square-testet.
print(chisq.test(iris.data))
R-utgång:
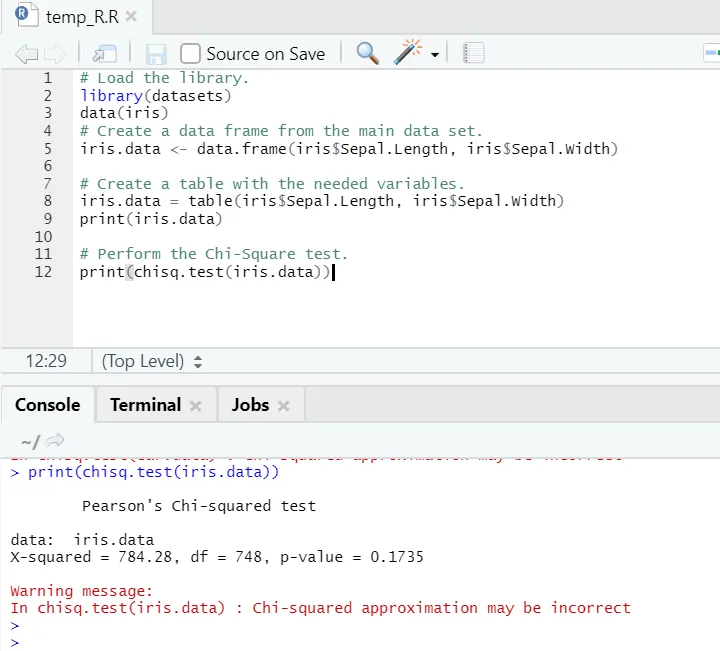
Som man kan se har chi-square-testet utförts över ett iris-datasätt med tanke på dess två variabler “Sepal. Längd ”och“ Sepal.Width ”.
P-värdet är inte mindre än 0, 05, därför finns det inte korrelation mellan dessa två variabler. Eller så kan vi säga att dessa två variabler inte är beroende av varandra.
Slutsats
Funktioner i R är enkla, enkla att anpassa, enkla att förstå och ändå mycket kraftfulla. Vi såg en mängd olika funktioner som används som en del av grunderna i R. När man väl blir bekväm med dessa funktioner som diskuterats ovan kan man utforska andra variationer av funktioner. Funktioner hjälper dig att göra din kod kör på ett enkelt och kortfattat sätt. Funktioner kan vara inbyggda eller användardefinierade, allt beror på behovet när man tar upp ett problem. Funktioner ger en bra form till ett program.
Rekommenderade artiklar
Detta är en guide till funktioner i R. här diskuterar vi hur man skriver funktioner i R och olika typer av funktioner i R med syntax och exempel. Du kan också titta på följande artikel för att lära dig mer -
- R Strängfunktioner
- SQL-strängfunktioner
- T-SQL-strängfunktioner
- PostgreSQL-strängfunktioner