
Introduktion till DFS-algoritm
DFS är känd som Djup första sökalgoritmen som ger stegen att korsa varje nod i en graf utan att upprepa någon nod. Denna algoritm är densamma som Depth First Traversal för ett träd men skiljer sig i att upprätthålla en boolesisk för att kontrollera om noden redan har besökts eller inte. Detta är viktigt för grafkorsning eftersom cykler också finns i grafen. En stack bibehålls i denna algoritm för att lagra de upphängda noderna medan de går igenom. Det heter det för att vi först reser till djupet för varje angränsande nod och sedan fortsätter att korsa en annan angränsande nod.
Förklara DFS-algoritmen
Denna algoritm strider mot BFS-algoritmen där alla angränsande noder besöks följt av grannar till de angränsande noderna. Det börjar utforska diagrammet från en nod och undersöker dess djup innan backtracking. Två saker beaktas i denna algoritm:
- Besöka en toppunkt: Val av en toppunkt eller nod på grafen för att korsa.
- Utforskning av en toppunkt: Korsa alla noder som gränsar till det toppunktet.
Pseudokod för djup Första sökning :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Linear Traversal finns också för DFS som kan implementeras på tre sätt:
- Förboka
- I ordning
- Postorder
Omvänd postorder är ett mycket användbart sätt att korsa och användas vid topologisk sortering samt olika analyser. En bunt upprätthålls också för att lagra de noder vars utforskning fortfarande är pågående.
Graf Traverse i DFS
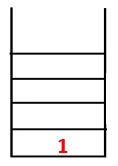
I DFS följs stegen nedan för att korsa grafen. Till exempel, en given graf, låt oss börja genomföra från 1:
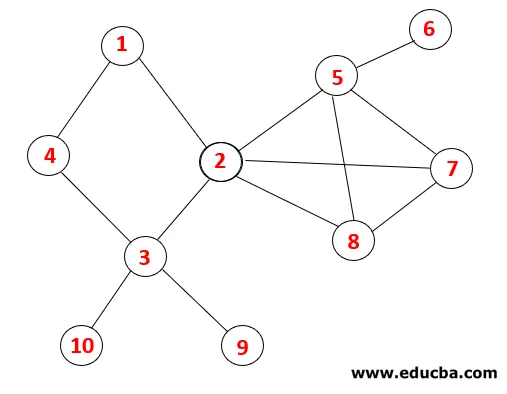
| Stack | Traversal Sequence | Spanning Tree |
| 1 |  |
|
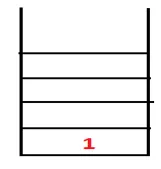 | 1, 4 |  |
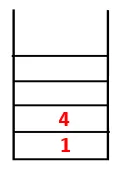 | 1, 4, 3 |  |
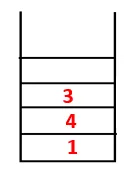 | 1, 4, 3, 10 | 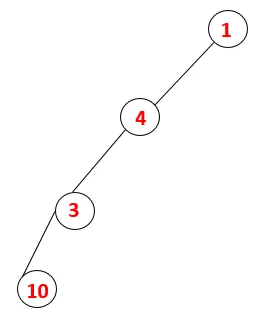 |
 | 1, 4, 3, 10, 9 | 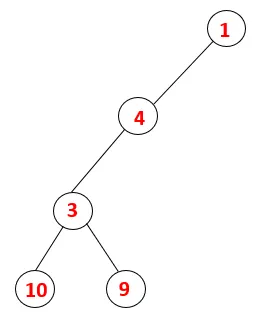 |
 | 1, 4, 3, 10, 9, 2 | 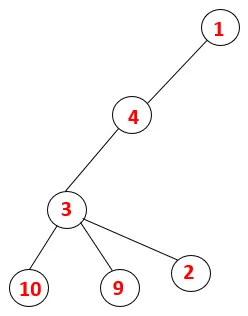 |
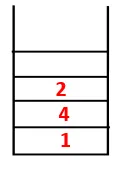 | 1, 4, 3, 10, 9, 2, 8 |  |
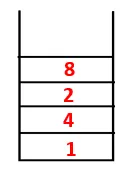 | 1, 4, 3, 10, 9, 2, 8, 7 | 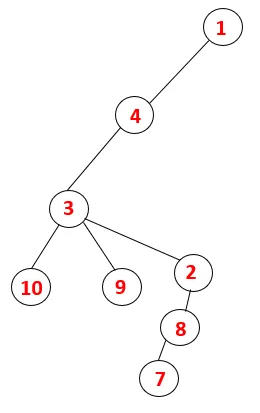 |
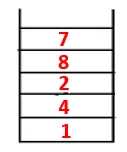 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
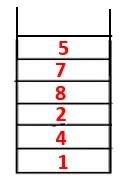 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 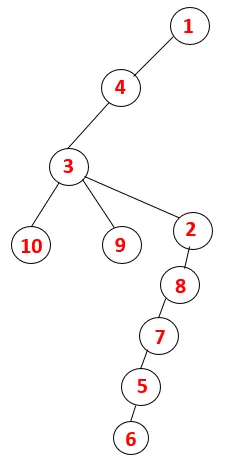 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 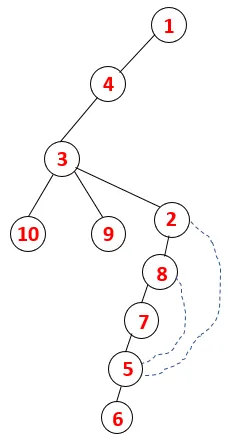 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
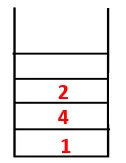 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 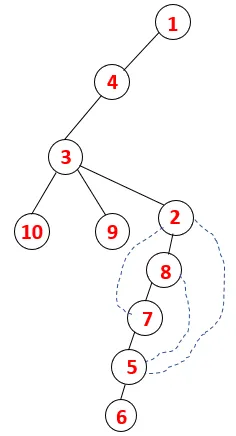 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 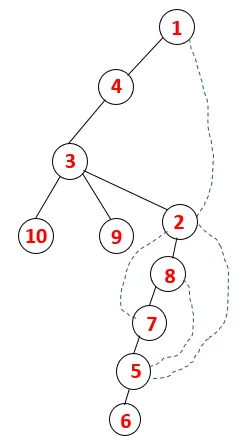 |
Förklaring till DFS-algoritm
Nedan följer stegen till DFS Algoritm med fördelar och nackdelar:
Steg 1: Nod 1 besöks och läggs till i sekvensen såväl som det spännande trädet.
Steg 2: Intilliggande noder av 1 utforskas som är 4, varför 1 skjuts till stapeln och 4 skjuts in i sekvensen såväl som spännträdet.
Steg 3: En av de angränsande noderna för 4 utforskas och därmed skjuts 4 till bunten, och 3 går in i sekvensen och det spännande trädet.
Steg 4: Intilliggande noder av 3 utforskas genom att trycka den på bunten och 10 kommer in i sekvensen. Eftersom det inte finns någon angränsande nod till 10, slås således 3 ut ur bunten.
Steg 5: En annan angränsande nod av 3 utforskas och 3 skjuts på bunten och 9 besöks. Ingen angränsande nod på 9 sålunda 3 poppas ut och den sista angränsande noden på 3 dvs. 2 besökas.
Liknande process följs för alla noder tills stacken blir tom vilket indikerar stoppvillkoren för genomgångsalgoritmen. - -> Prickade linjer i spännträdet hänvisar till bakkanterna som finns i diagrammet.
På detta sätt går alla noderna i diagrammet utan att upprepa någon av noderna.
Fördelar och nackdelar
- Fördelar: Det här minneskravet för denna algoritm är mycket mindre. Mindre utrymme och tidskomplexitet än BFS.
- Nackdelar: Lösning garanteras inte. Topologisk sortering. Hitta grafbroar.
Exempel på implementering av DFS-algoritm
Nedan är exemplet för implementering av DFS-algoritm:
Koda:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Produktion:
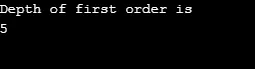
Förklaring till ovanstående program: Vi gjorde en kurva med 5 vertikaler (0, 1, 2, 3, 4) och använde besökt array för att hålla reda på alla besökta toppar. Sedan upprepas för varje nod vars angränsande noder finns samma algoritm tills alla noderna har besökts. Sedan går algoritmen tillbaka till att ringa vertex och poppa den från stacken.
Slutsats
Minneskravet för denna graf är mindre jämfört med BFS eftersom endast en stack behövs för att upprätthållas. Ett DFS-spännsträd och en korsningssekvens genereras som ett resultat men är inte konstant. Flera traversalsekvenser är möjliga beroende på det valda startpunktet och undersökningsvinkeln.
Rekommenderade artiklar
Detta är en guide till DFS-algoritm. Här diskuterar vi steg för steg förklaring, korsa diagrammet i ett tabellformat med fördelar och nackdelar. Du kan också gå igenom våra andra relaterade artiklar för att lära dig mer -
- Vad är HDFS?
- Deep Learning Algoritms
- HDFS-kommandon
- SHA-algoritm