Linjär interpolering i Excel (innehållsförteckning)
- Vad är interpolering?
- Interpolation med prognosfunktion i Excel
- Exempel på linjär interpolering i Excel
Vad är interpolering?
I matematikens värld är interpolering en metod för att skapa nya datapunkter med hjälp av kända datapunkter. Interpolering uppskattar värdet baserat på befintliga tillgängliga datavärden som är relatabla.
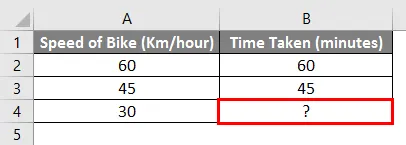
Till exempel - Om vi kör en cykel på 60 km / timme och nådde en viss destination på 1 timme och om vi kör på 45 km / timme och nådde en viss destination på 45 minuter. Så hur lång tid tar det att nå en destination om vi kör på 30 km / timme.
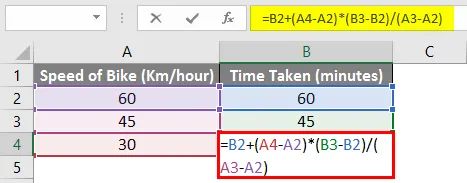
Med enkel matematik kan vi beräkna de saknade värdena i exemplet ovan. Vi måste infoga formeln nedan i cell B4.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Så på grundval av ovanstående formel kan vi säga att det tar 30 minuter att nå målet om vi kör med 30 km / timme.
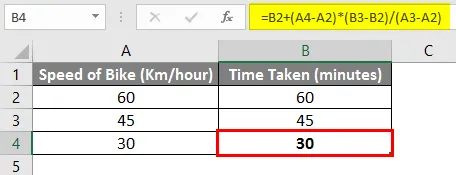
Låt oss försöka bryta ovanstående formel och förstå formeln i detalj.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
I exemplet ovan beräknar den sista delen av formeln som markeras med rött hur mycket tid det tar förändras när cykelns hastighet ändras med 1. I vårt exempel ändras tiden som tar 1 minut när cykelns hastighet ändras med 1 km /timme.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Det andra avsnittet (i blått ovan) beräknar hur långt vår cykelhastighet är borta från den angivna första hastigheten på cykeln multiplicerar den sedan med det värde som beräknats ovan. Baserat på vårt exempel är det 30 (Cell A4) minus 60 (Cell A2), vars resultat sedan multipliceras med 1 (vilket motsvarar -30).
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Slutligen den första delen av formeln (i brunt ovan); lägger vi till det första värdet på cykelns hastighet. I vårt exempel ger detta slutresultatet av 60 + (-30) * (1) = 30 minuter. I skolan använde vi formeln nedan för att beräkna det saknade värdet på Y.
Y = Y1 + (X-X1) * (Y2-Y1) / (X2 - X1)
Detta är ett exempel på hur man beräknar de saknade värdena med hjälp av en manuell formel för att förstå interpolering.
Excel har en inbyggd funktion som gör en liknande beräkning som ovan och den kallas FORECAST-funktion. Nu kommer vi att lära oss den här funktionen i detalj nu.
Interpolering med prognosfunktion i Excel
Prognos är en kalkylfunktion som finns i MS Excel och använder linjär regression för att ta reda på det saknade värdet. Prognos som namnet antyder att den används för att förutse det framtida värdet för en datapunkt, men det kan också användas för att interpolera ett värde. I grund och botten används det för att beräkna det framtida värdet baserat på befintliga värden för en specifik datauppsättning.
Syntax för prognosfunktion

Argument för prognos funktion:
- x - Det är en datapunkt för vilken vi vill veta det resulterande värdet.
- Known_y's - Cellintervall som innehåller värdena för Y.
- Known_x's - Cellintervall som innehåller värdena för X.
Nu när vi överväger samma exempel ovan, låt oss försöka använda prognosfunktionen.
I vårt exempel,
x - Cell B4 (eftersom vi vill ta reda på vilken tid det tar när hastigheten på 30 km / timme).
Known_y's - Cell B2 till Cell B3 (Det tar tid för den kända hastigheten på cykeln).
Known_x's - Cell A2 till Cell A3 (hastigheten på den cykel som redan har givits för vilken vi vet vilken tid det tar).
Så den slutliga formeln i cell B4 kommer att vara som nedan:
= PREDIKTION (A4, B2: B3, A2: A3)
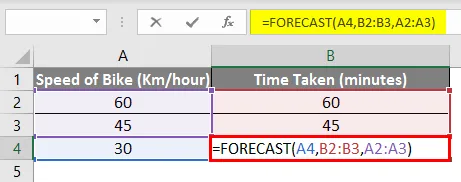
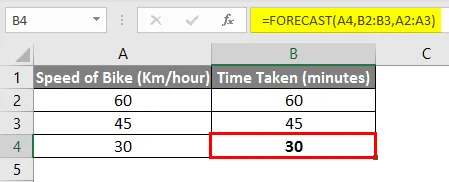
Och som ni kan se är slutresultatet detsamma, dvs. 30 minuter .
För att skapa ett diagram, gå till Infoga-menyn, klicka på Scatter och välj sedan Scatter With Smooth Lines and Markers.
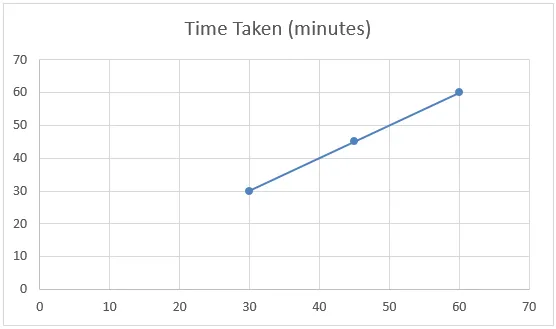
Om vi tittar på diagrammet nedan i exemplet ovan kan vi säga att datauppsättningen har en linjär relation och kallas linjär interpolering.
Exempel på linjär interpolering i Excel
Låt oss förstå den linjära interpolationen i Excel med några exempel.
Du kan ladda ner den här linjära interpolationsmallen för Excel här - Linjär interpolering av Excel-mallExempel 1
Anta att du har försäljnings- och vinstdata för tidigare år och att du vill veta resultatet för innevarande år om du uppnår en viss försäljningsnivå.
Titta på tabellen nedan. Du har försäljningsdata från 2016 till 2018 och du vill veta vad som ska vara vinsten om din försäljning är Rs. 40, 00 000 år 2019.
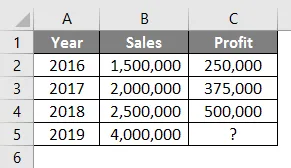
Så med hjälp av Forecast-funktionen kan vi interpolera vinsten från 2019 när försäljningen är Rs. 4.000.000
Formeln i cell C5 kommer att vara som nedan:
= Prognos (B5, C2: C4, B2: B4)
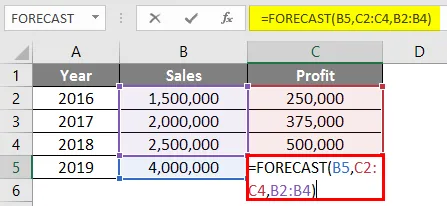
Efter att ha använt prognosformel, svaret nedan.
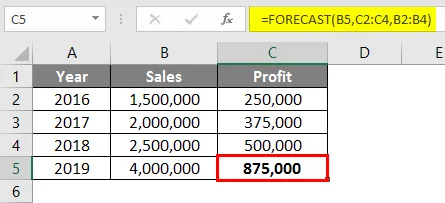
Resultatet för prognosfunktionen blir Rs. 875 000 baserat på försäljnings- och vinstdata från 2016 till 2018.
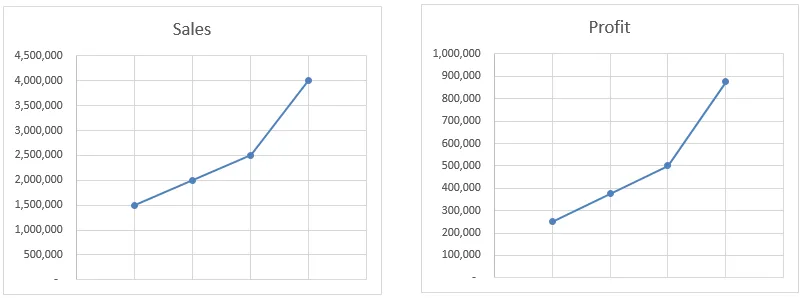
I det här exemplet interpolerar prognosfunktionen värdet baserat på all tillgänglig data och inte bara start- och slutpunkt. Som ni ser i diagrammen är rörelsevinsten exakt densamma som försäljning. Även om vi beräknar värdet manuellt kommer det fortfarande att ge oss samma resultat.
Exempel 2
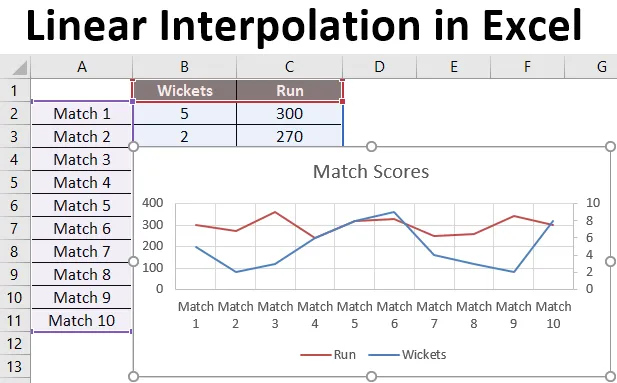
Vi har data om de sista nio matcherna i cricketlaget som har gått wickets och kört poäng av laget.
Vi vill ta reda på hur många körningar som får lagpoäng om 8 wickets faller.
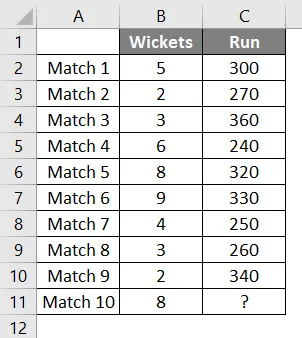
Så vi kommer att använda samma prognosfunktion som ovan.
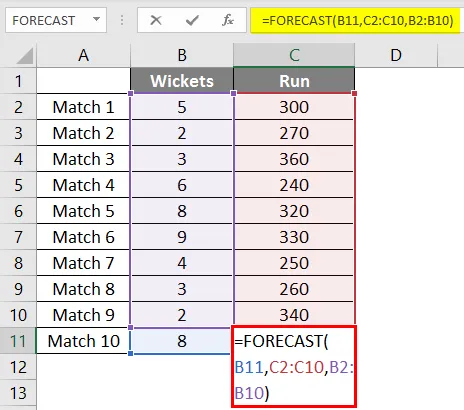
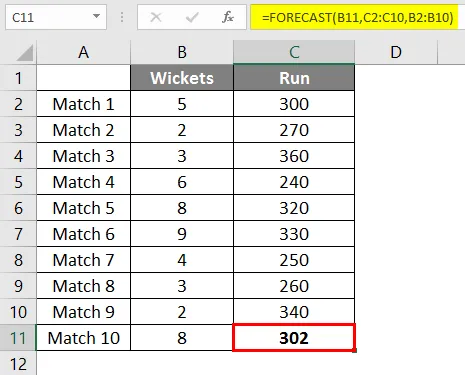
Efter att ha använt formeln får vi resultatet av 302 körningar om vi 8 wickets faller på grundval av en linjär regression av de senaste 9 matcherna som spelas av laget.
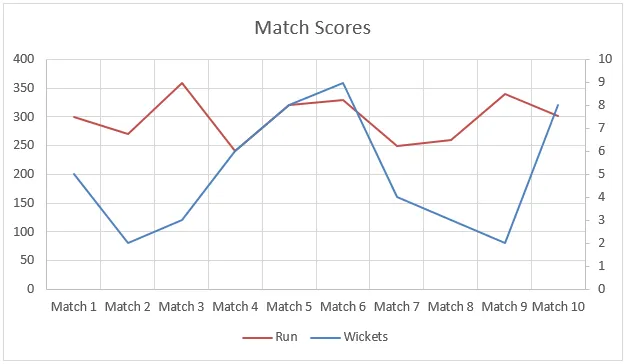
I det här exemplet var data inte linjära och du kan se det i diagrammet nedan. Men ändå hjälpte Prognosfunktionen oss att interpolera körningarna med hjälp av data från tidigare matcher.
Saker att komma ihåg om linjär interpolering i Excel
- Prognosfunktion används för att förutse / uppskatta värdet baserat på befintliga tillgängliga värden men det kan också hjälpa till att interpolera det saknade värdet.
- Om data inte är linjära ger Prognosfunktionen dig inte det exakta värdet som är baserat på linjär interpolering men den ger dig det närmaste värdet.
- Om x i prognosfunktionen är text eller icke-numerisk, returnerar prognosfunktionen #VALUE-felet.
- Om Known_x och Known_y's inte innehåller några data eller innehåller en annan uppsättning datapunkter, kommer Prognosfunktion att ge ett # N / A-fel.
- Om variansen mellan Known_x är noll ger Prognosfunktionen felet # DIV / O.
Rekommenderade artiklar
Detta är en guide till linjär interpolering i Excel. Här diskuterar vi hur man använder linjär interpolering i Excel tillsammans med praktiska exempel och nedladdningsbar Excel-mall. Du kan också gå igenom våra andra föreslagna artiklar -
- Linjär regression i Excel
- Sök efter text i Excel
- Textformel i Excel
- Marimekko diagram Excel
- Interpolera i Excel
- Linjär programmering i Excel