
Introduktion till matematiska funktioner i C
Den här artikeln visar de olika matematiska funktionerna som används i C-programmeringsspråk med illustration av arbetskod. Datorer gör enorma matematiska beräkningar och analyser av enormt antal, för att göra det har vi använt matematiska funktioner i C. Innan vi börjar måste vi veta att C-språk använder rubrik / bibliotek som heter Math.h för olika matematiska funktioner. Detta hjälper till att beräkna trigonometriska operationer, logaritmer, absoluta värden, kvadratrot. Så låt oss utforska de olika typerna av funktioner som används i detta bibliotek. Alla dessa funktioner är dubbla som datatyp och returnerar samma.
Olika matematiska funktioner i C.
Låt oss se olika funktioner som definieras i matematik. Matematikbiblioteket kategoriseras i tre huvudtyper: Trigonometriska funktioner, matematikfunktioner, Log / expo-funktioner. För att implementera funktionerna nedan är det obligatoriskt att inkludera eller i koden.
1. våning (dubbel a)
Denna funktion returnerar det största heltalvärdet som inte är större än 'a'. Det avrundar ett värde och returnerar en dubbel som resultat. Det fungerar annorlunda för negativa siffror eftersom de avrundar till nästa negativa nummer.
Ex: golv (7, 2) är 7, 0
golv (-7, 2) är -8, 0
Exempel:
Detta program illustrerar hur man beräknar golvet för det deklarerade värdet och avrundar till nästa värde 10.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
Produktion:

2. tak ()
Syntax:
double ceil (double b)
Denna funktion returnerar det minsta heltal som är större eller lika med b och avrundar värdet uppåt. För ett negativt värde rör sig det mot vänster. Exempel 3.4 returnerar -3 har utgången.
Exempel:
Detta program förklarar genom att mata in float-argumentet och returnerar takvärdet.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
Produktion:

3. Sqrt ()
Denna funktion returnerar kvadratroten till ett specificerat nummer.
Syntax:
sqrt( arg)
Exempel:
Koden nedan förklarar den mest kända matematiska funktionen sqrt () genom att ta 'n' värden för att beräkna kvadratroten för de olika 'n' värdena.
#include
#include
int main()
(
double n, output;
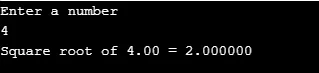
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
Produktion:
4. runda ()
Denna funktion avrundar det närmaste värdet på en given ingång. Det slänger ut felet om värdet är för stort. Andra funktioner som lround (), llround () avrundar också närmaste heltal.
Syntax:
int round(arg)
Exempel:
Nedanstående kod är mycket enkel, vilket avrundar till närmaste 'r' -värde i for-loopen.
#include
#include
int main ()
(
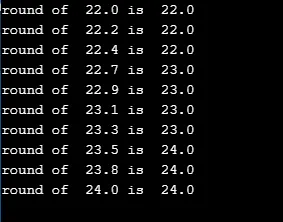
for(double r=110;r<=120;r+=1.1)
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
Produktion:
5. kraft ()
Denna funktion återgår till ström för det givna numret (a b ). Den returnerar en höjd till kraften hos b, som har två parametrar bas och exponent.
Exempel:
I källkoden nedan tillåter vi en användare att ange ett inmatningsvärde för att beräkna kraften för de givna två argumenten.
#include
#include
int main()
(
int r, ba, expr;
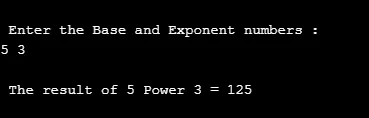
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
produktion:
6. trun ()
Denna funktion hjälper till att trunka det givna värdet. Det returnerar heltal. För att avkorta flytande och dubbla värden trunkf () används truncl ().
Syntax:
double trunc(a);
Exempel:
Nedan källkoden tar två inmatningsvärden a, b för att avkorta de dubbla värdena.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
Produktion:

7. fmod ()
Denna funktion returnerar återstoden för de givna två ingångsvärdena när m delas med n.
Syntax:
double fmod(double I, double j)
Exempel:
I exemplet nedan tar det två värden från användaren att beräkna resten med funktionen fmod ().
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
Produktion:

Trigonometriska funktioner
Nedan är de olika funktionerna för Trigonometric:
1. synd ()
Denna inbyggda funktion ger sinusvärde för det givna antalet, beräknar flytpunktsvärden. asin () beräknar båge, för hyperbolisk är det sinh ().
Syntax:
return type sin(y);
y returnerar värde i radianer och returtyp tar dubbelt.
Exempel:
I följande källkod har jag tagit två olika inmatningsvärden för att beräkna sinvärde och returnerar dubbel.
#include
#include
int main()
(
double a;
double z;
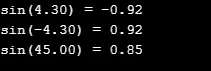
a = 4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
Produktion:
2. sinh ()
Denna matematikfunktion beräknar trigonometriskt tangent-sinusvärde för det givna antalet.
Syntax:
double sinh(x);
Exempel
I källkoden nedan beräknas Sine-hyperbolik genom att deklarera ett ingångsvärde.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
Produktion

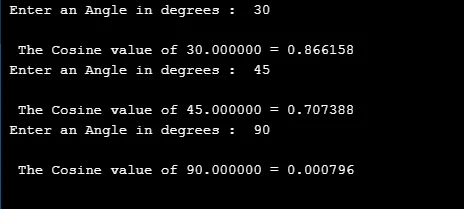
3. cos ()
Denna matematikfunktion bestämmer det trigonometriska kosinusvärdet för det givna elementet.
Syntax: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
Produktion:
4. kosh ()
Den returnerar hyberbolisk kosinus för ett visst värde.
Syntax:
double cosh(y);
Exempel
Exemplet nedan visar att det krävs två olika inmatningsvärden för att beräkna hyperboll.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
Produktion

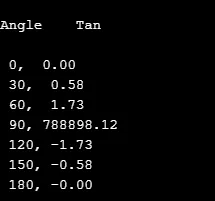
5. solbränna ()
Denna matematikbiblioteksfunktion beräknar tangensvärden för vinkeln för det matematiska uttrycket och mäts i radianer.
Det kan förklaras som
double tan(arguments);
Exempel
I följande källkod beräknas solvärdet för följande vinklar som ökas med hjälp av för slinga.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
Produktion:
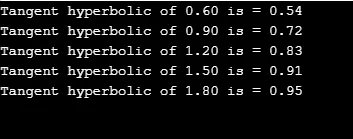
6. tanh ()
funktionen tanh () returnerar hyperbolisk tangens för det givna värdet. Det tar en enda parameter. Förutom att hitta tangens för lång dubbel och float tanhl () och tanhf () används för beräkning.
Syntax:
double tanh( val);
Exempel:
En tangenthyberbolik beräknas för "j" -värden som används för slingor. Låt oss se hur det fungerar.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
Produktion:
Log aritmetiska funktioner
Nedan är de olika funktionerna för log aritmetik:
1. exp ()
Denna funktion gör beräkningar på exponentiellt för ett givet värde (e x ). Det finns också andra subtyper som frexp (), Idexp () som returnerar mantissa och multipliceras till kraften i x.
Syntax:
return type exp(value);
Exempel:
Programmet tar numeriskt värde från användaren för att beräkna exponenten för ett givet värde och returnerar dubbel.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
Produktion

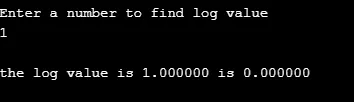
2. logg ()
Denna funktion returnerar logaritmvärdet för ett givet nummer. (till basen e. log e )
Syntax:
double log(arg);
Exempel:
I följande exempel beräknas loggvärdet för det givna numret med funktion. Användardefinierad funktion lgm () gör beräkning och funktion kallas i huvudfunktionen.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
produktion:
Slutsats
Avslutningsvis har vi sett olika matematiska funktioner som används i C-programmering och det är de direkta biblioteksfunktioner som ska användas. C-program använder dessa funktioner för olika matematiska operationer. För att lösa vissa komplexa versioner av beräkningar gynnar denna inbyggda funktion matematiskt orienterade programmeringsspråk för att returnera enkla värden.
Rekommenderade artiklar
Detta är en guide till matematiska funktioner i C. Här diskuterar vi olika matematiska funktioner i C med exempel. Du kan också gå igenom våra andra föreslagna artiklar -
- PHP Matematiska funktioner
- JavaScript-matematiska funktioner
- Överför funktioner i Matlab
- JavaScript-strängfunktioner
- Introduktion till matematiska funktioner i Python
- Översikt över matematiska funktioner i C #
- C Programmering av matrismultiplikation
- Square Root i PHP
- Exempel på Square Root i JavaScript