
Introduktion till Sortera i JavaScript
Sorteringsalgoritmer är mycket viktiga inom datavetenskap. Utmatningen från sorteringen är att ordna elementen i en lista i en viss ordning (antingen stigande eller fallande). Merge Sort in JavaScript är en av de mest effektiva sorteringsalgoritmerna som finns tillgängliga eftersom den är baserad på begreppet split och erövrar. Som namnet antyder, dela först det större problemet i små problem än att lösa de mindre problemen för att lösa det större problemet. Konceptuellt är Merge sort en kombination av två grundläggande algoritmer som kallas MERGE och MERGE_SORT.
som fungerar enligt följande:
- Dela upp den osorterade listan i n-nummer av undelistor med en artikel (n är det totala antalet element i den osorterade listan).
- Slå samman sublister upprepade gånger i sorterade underlistor tills det bara finns en sorterad lista.
Implementering av Sortera i JavaScript
MERGE-algoritmen följer proceduren för att kombinera två sorterade listor till en sorterad lista.
Exempel: Anta att det finns två listor, dvs. lista 1 (1, 5, 3) och lista 2 (7, 2, 9).
1. Sortera först båda listorna.
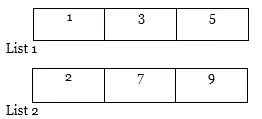
Nu kommer vi att se och tillämpa E-tekniken på den.
2. Då skapar vi en ny lista med storlek x + y där x är antalet element i lista 1 och y är antalet element i lista 2.

I vårt fall x = 3 och y = 3, så x + y = 6.
3. Nu har vi två pekare.
En första pekare som pekar på den första positionen i lista 1 och den andra pekaren som pekar på den första positionen i lista 2.

4. Sedan jämför vi värdet på båda pekarna. Pekaren med mindre värde, kopiera det elementet till lista 3 och flytta pekaren till höger om listan med mindre värde och den resulterande listan (dvs. lista 1 och lista 3)

5. Utför på samma sätt steg 4 igen och igen.

Ytterligare korsa …
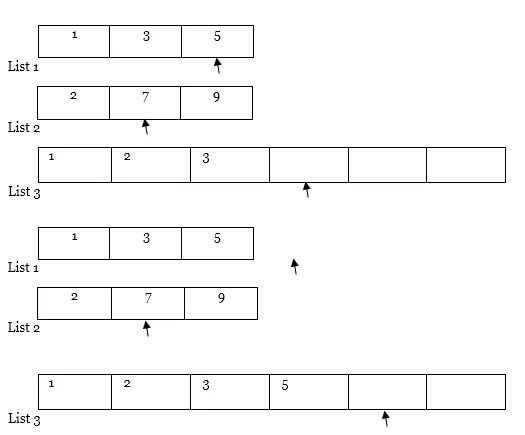
Obs : Om en av listorna (dvs. lista 1 eller lista 2) blir fullständigt korsad som i fallet, kopierar du hela innehållet i en annan lista från pekaren till resultatlistan (dvs. lista 3) enligt följande.

pseudo
Function merge (sublist1, sublist2) (
Create var for result list
While sublist1 length > 0 and sublist2 length > 0
If sublist1(0) < sublist2(0) Copy the sublist1 pointer value to result list and Shift pointer of sublist1 to right
else
Copy the sublist2 pointer value to result list and Shift pointer of sublist2 to right
Return concat sublist1 or sublist2 (depending if node1 is empty or not)
MERGE_SORT-algoritmen delar upp den givna osorterade listan i minsta storlek och kallar sedan MERGE-algoritmen för att kombinera listan i den nya sorterade listan.
pseudo
function mergeSort(list) (
If list length < 2
Return list
Create var for middle index of list
Create var for left index of list
Create var for right index of list
Recursively call mergeSort function
)
Exempel
Här följer vi nedföljande implementering av Merge Sort. Det börjar överst och fortsätter mot nedåt, med varje rekursiv sväng som ställer samma fråga "Vad krävs för att sortera listan?" Och med svaret är "Dela listan i två, ring ett rekursivt samtal och slå samman resultat".
Kod i Javascript
// Split the list into halves and merge them recursively
function mergeSort (list) (
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
var mid = Math.floor(list.length / 2);
var left = mergeSort(list.slice(0, mid));
var right = mergeSort(list.slice(mid));
return merge(left, right);
)
// compare the lists element by element and return the concatenated resultList
function merge (sublist1, sublist2) (
var resultList = ();
while (sublist1.length > 0 && sublist2.length > 0)
resultList.push(sublist1(0) < sublist2(0)? sublist1.shift() : sublist2.shift());
return resultList.concat(sublist1.length? sublist1 : sublist2);
)
const list = (6, 5, 3, 1, 8, 7, 2, 4, 2, 5, 1, 2, 3) console.log(mergeSort(list)) //( 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8 )
Huvudfunktionen för sammanslagningssorteringen kommer att dela upp den givna listan i mindre listor i varje iteration av det rekursiva samtalet. Glöm inte att rekursion kräver basvillkoret för att undvika oändlig rekursion. I vårt fall har vi:
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
När vi har ställt in basvillkoret för rekursion, identifierar vi mittindex för att dela upp den givna listan i vänster och höger underlista, som du kan se ovan i exempeldiagrammet. Då måste vi slå samman den vänstra undelistan och den högra undelistan som vi ser nu. I fusionsfunktionen ovan måste vi se till att vi sorterar alla element i den vänstra undelistan och den högra under- lista. Så vi gör detta är att använda en stundslinga. Inom medan-loopen kommer vi att jämföra elementet i den vänstra underlistan och elementet i den högra underlistan en efter en. Vi kan trycka in den minsta av de två i resultatlistan och flytta markören för den vänstra underlistan och den högra underlistan i enlighet därmed. Slutligen måste vi sammanfoga resultatlistan. Det här är väldigt viktigt! Om vi inte gör det sista steget här, kommer vi att ha en ofullständig lista över element i slutet eftersom villkoret för medan loopen kommer att misslyckas när någon av de två pekarna når slutet.
Produktion:

Egenskaper för sammanslagningssortering
- Sammanfogningssortering är stabil eftersom samma element i en matris upprätthåller sina ursprungliga positioner i förhållande till varandra.
- Slå samman sortering är inte "på plats" eftersom det under en sammanslagning skapar en kopia av hela listan sorteras. På grund av detta är rymdkomplexiteten (O (n)) för denna algoritm faktiskt större än andra, och ska inte användas i komplexa problem där utrymmet är premium.
- Den övergripande tidskomplexiteten för Merge sort är O (nLogn). Det är mer effektivt eftersom det i värsta fall också är körtiden O (nlogn).
Slutsats
Slå samman bästa, sämsta och genomsnittliga tidskomplexiteten är desamma som gör det till en effektivare algoritm. Det fungerar snabbare än andra sorteringstekniker. Sorteringssortering kan tillämpas på filer av valfri storlek. Den är mycket parallelliserbar på grund av användningen av divide-and-conquer-metoden. För att utveckla starka grunder i datavetenskap rekommenderas du att förstå grundligt olika sorteringsalgoritmer.
Rekommenderad artikel
Detta har varit en guide till Slå samman i JavaScript. Här diskuterar vi Introduktion till sammanslagningssortering i JavaScript och implementeringen tillsammans med Egenskaper. Du kan också gå igenom våra andra föreslagna artiklar för att lära dig mer -
- JavaScript-matematiska funktioner
- Introduktion till JavaScript
- Bästa Javascript-ramverk
- JavaScript-verktyg
- Topp 6 sorteringsalgoritm i JavaScript