Introduktion till hierarkisk klustering
- Nyligen bad en av våra kunder vårt team att ta fram en lista över segment med en ordning av betydelse inom sina kunder för att rikta dem till att franchisera en av sina nyligen lanserade produkter. Det är tydligt att bara segmentera kunderna med hjälp av partiell gruppering (k-medel, c-fuzzy) kommer inte att få fram den vikt som det är där hierarkisk kluster kommer in i bilden.
- Hierarkisk klustering delar upp data i olika grupper baserat på vissa likhetsåtgärder kända som kluster, som i huvudsak syftar till att bygga hierarkin bland kluster. Det är i princip oövervakat lärande och att välja attribut för att mäta likhet är applikationsspecifikt.
Cluster of Data Hierarchy
- Agglomerativ gruppering
- Divisiv Clustering
Låt oss ta ett exempel på data, betyg som erhållits av 5 elever för att gruppera dem för en kommande tävling.
| Studerande | Marks |
| EN | 10 |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35s |
1. Agglomerativ klustering
- Till att börja med betraktar vi varje enskild punkt / element här vikt som kluster och fortsätter att slå samman de liknande punkterna / elementen för att bilda ett nytt kluster på den nya nivån tills vi sitter kvar med det enda klustret är en bottom-up-strategi.
- Enkel koppling och fullständig koppling är två populära exempel på agglomerativ gruppering. Annat än den genomsnittliga kopplingen och Centroid-kopplingen. I en enda koppling sammanfogar vi i varje steg de två klusterna, vars två närmaste medlemmar har det minsta avståndet. I komplett koppling sammanfogar vi medlemmarna i det minsta avståndet som ger det minsta maximala parvisa avståndet.
- Närhetsmatris, det är kärnan för att utföra hierarkisk gruppering, som ger avståndet mellan var och en av punkterna.
- Låt oss skapa närhetsmatris för våra data som anges i tabellen, eftersom vi beräknar avståndet mellan var och en av punkterna med andra punkter kommer det att vara en asymmetrisk matris med form n × n, i vårt fall 5 × 5 matriser.
En populär metod för avståndsberäkningar är:
- Euklidiskt avstånd (kvadrat)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Manhattan avstånd
dist((x, y), (a, b)) =|x−c|+|y−d|
Euklidiskt avstånd används oftast, vi kommer att använda det här här och vi kommer att gå med komplex koppling.
| Elev (Clusters) | EN | B | C | D | E |
| EN | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Diagonala element i närhetsmatrisen kommer alltid att vara 0, eftersom avståndet mellan punkten med samma punkt alltid är 0, varför diagonala element undantas från hänsyn till gruppering.
Här, i iteration 1, är det minsta avståndet 3, varför vi sammanfogar A och B för att bilda ett kluster, bildar igen en ny närhetsmatris med kluster (A, B) genom att ta (A, B) klusterpunkt som 10, dvs. maximalt ( 7, 10) så nybildad närhetsmatris skulle vara
| kluster | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
I iteration 2, 7 är det minsta avståndet, varför vi sammanfogar C och E och bildar ett nytt kluster (C, E), vi upprepar processen som följs i iteration 1 tills vi hamnar med det enda klustret, här stannar vi vid iteration 4.
Hela processen visas i figuren nedan:
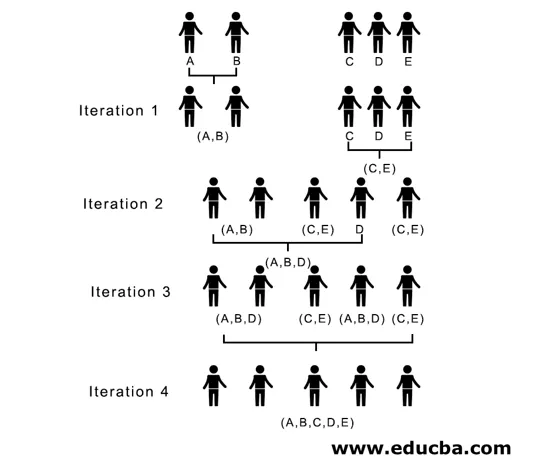
(A, B, D) och (D, E) är de två kluster som bildas vid iteration 3, vid den sista iterationen kan vi se att vi sitter kvar med ett enda kluster.
2. Delande kluster
Till att börja med betraktar vi alla punkter som ett enda kluster och separerar dem längst bort tills vi slutar med enskilda poäng som enskilda kluster (inte nödvändigtvis kan vi stoppa i mitten, beror på det minsta antalet element vi vill ha i varje kluster) vid varje steg. Det är precis motsatsen till agglomerativ gruppering och det är en top-down-strategi. Delande kluster är ett sätt som repetitiva k betyder kluster.
Att välja mellan Agglomerative och Divisive Clustering är igen applikationsberoende, men få punkter som ska beaktas är:
- Divisive är mer komplex än agglomerativ gruppering.
- Uppdelande kluster är mer effektiv om vi inte genererar en fullständig hierarki ner till enskilda datapunkter.
- Agglomerativ klustering fattar ett beslut genom att ta hänsyn till de lokala klapparna utan att ta hänsyn till globala mönster från början som inte kan vändas.
Visualisering av hierarkisk klustering
En super användbar metod för att visualisera hierarkisk kluster som hjälper till i affärer är Dendogram. Dendogram är trädliknande strukturer som registrerar sekvensen av sammanslagningar och uppdelningar där vertikala linjer representerar avståndet mellan klusterna, avståndet mellan vertikala linjer och avståndet mellan klusterna är direkt proportionella, dvs mer avståndet mer kluster kommer sannolikt att vara olika.
Vi kan använda dendogrammet för att bestämma antalet kluster, bara rita en linje som korsar en längsta vertikala linje på dendogrammet, ett antal vertikala linjer som korsas kommer att vara antalet kluster som ska beaktas.
Nedan visas exemplet Dendogram.
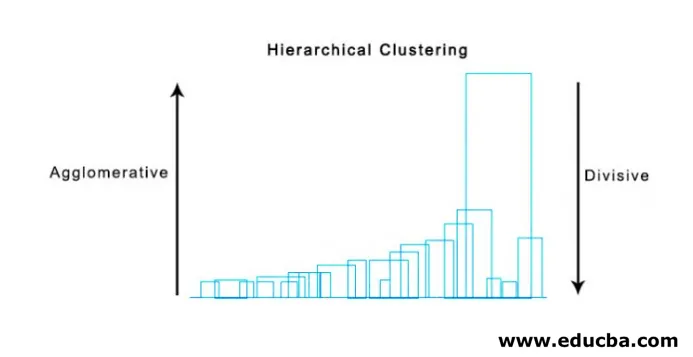
Det finns ganska enkla och direkta pythonpaket och det är funktioner för att utföra hierarkisk klustering och plotta dendogram.
- Hierarkin från scipy.
- Cluster.hierarchy.dendogram för visualisering.
Vanliga scenarier där hierarkisk kluster används
- Kundsegment till marknadsföring av produkter eller tjänster.
- Stadsplanering för att identifiera platserna att bygga strukturer / tjänster / byggnad.
- Sociala nätverksanalys, identifiera till exempel alla MS Dhoni-fans för att annonsera hans biopic.
Fördelar med hierarkisk klustering
Fördelarna ges nedan:
- När det gäller delvis kluster som k-medel bör antalet kluster vara kända före kluster, vilket inte är möjligt i praktiska tillämpningar, medan det i hierarkisk kluster inte krävs någon förkunskaper om antalet kluster.
- Hierarkisk gruppering avger en hierarki, dvs en struktur som är mer informativ än den ostrukturerade uppsättningen av de platta klusterna som återlämnats genom partiell klustering.
- Hierarkisk klustering är lätt att implementera.
- Visar resultat i de flesta scenarier.
Slutsats
Typ av gruppering gör den stora skillnaden när data presenteras, hierarkisk gruppering som är mer informativ och lätt att analysera är mer föredragen än partiell klustering. Och det är ofta förknippat med värmekartor. Att inte glömma attribut som väljs för att beräkna likhet eller skillnad påverkar främst både kluster och hierarki.
Rekommenderade artiklar
Detta är en guide till hierarkisk klustering. Här diskuterar vi introduktionen, fördelarna med Hierarchical Clustering och Common Scenarios där Hierarchical Clustering används. Du kan också gå igenom våra andra artiklar som föreslås för att lära dig mer–
- Clustering algoritm
- Clustering in Machine Learning
- Hierarkisk gruppering i R
- Clustering Methods
- Hur tar man bort hierarkin i Tableau?