
Introduktion till rutor i Java
När ett tal multipliceras med sig själv är det resulterande talet som bildas numretets kvadrat. Rutor med ett antal är mycket enkla att hitta. När vi hittar kvadratroten till ett heltal får vi resultatet bara i heltal. På samma sätt får vi svaret också i decimaler när vi hittar kvadratet med ett decimaltal. Ett intressant faktum med kvadratet på ett nummer är att när vi gör en kvadrat med ett heltal så ökar värdet på det resulterande antalet. Men när vi gör kvadratet med decimaler mellan 0 och 1, minskar det resulterande antalet. Ett exempel skulle vara en kvadrat på 0, 5. När vi kvadrerar 0, 5 sjunker antalet till 0, 25. I den här artikeln ska vi se de olika metoderna för hur vi kan kvadrera ett nummer med Java-programmeringsspråket.
Arbeta - Kvadrat med ett nummer kan hittas i Java med en mängd olika tekniker. Vi skulle vilja se några exempel relaterade till kvadratet med ett nummer som vi kan förstå kvadratet på ett nummer bättre.
Hur beräknar jag Square i Java?
Låt oss lära oss hur man beräknar kvadrat i java:
Exempel 1
Det enklaste sättet att hitta kvadratet på ett nummer är Math.pow () där det kan användas för att beräkna vilken effekt som helst för ett nummer.
Koda:
import java.util.*;
public class Square
(
public static void main(String args())
(
Scanner sc=new Scanner(System.in);
int num;
System.out.print("Enter a number which is integer format: ");
num=sc.nextInt();
System.out.println("The square of "+ num + " is: "+ Math.pow(num, 2));
)
)
Produktion:

Exempel 2
I nästa program kommer vi att beräkna kvadratet på ett tal i den vanliga formen så att det multiplicerar två siffror i följd och hittar kvadratet för respektive nummer.
Koda:
import java.util.*;
public class Square2
(
public static void main(String args())
(
Scanner sc=new Scanner(System.in);
int no;
System.out.print("Enter a number which is integer format: ");
no=sc.nextInt();
System.out.println("Square of "+ no + " is: "+(no*no));//the number is multiplied with its own
)
)
Produktion:

Exempel 3
I det här exemplet kommer vi att kontrollera om ett tal är ett perfekt fyrkant eller inte. Detta är lite komplicerat program eftersom det kontrollerar om ett nummer är en kvadrat med ett annat nummer.
Koda:
import java.util.Scanner;
class JavaExample (
static boolean checkPerfectSquare(double x)
(
// finding the square root of given number
double s= Math.sqrt(x);
return ((s - Math.floor(s)) == 0); //Math.floor() is used here to calculate the lower value.
)
public static void main(String() args)
(
System.out.print("Enter any number:");
Scanner scanner = new Scanner(System.in);
double no= scanner.nextDouble();
scanner.close();
if (checkPerfectSquare(no))
System.out.print(no+ " is a perfect square number");
else
System.out.print(no+ " is not a perfect square number");
)
)
Produktion:

Exempel 4
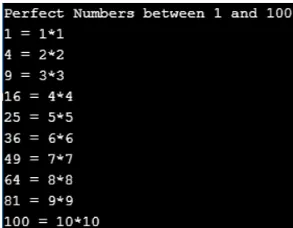
I det här programmet hittar vi antalet kvadratiska nummer inom ett specifikt intervall. Vi anger antalet och koden skulle producera kvadratnumret i det specifika intervallet. I nedanstående program hittar vi antalet fyrkantiga heltal mellan 0 och 100.
Koda:
// Finding the range of perfect square numbers in Java programming language
import java.io.IOException;
public class SquareNumbersInRange (
public static void main(String() args) throws IOException (
int starting_number = 1;
int ending_number = 100;
System.out.println("Perfect Numbers between "+starting_number+ " and "+ending_number);
for (int i = starting_number; i <= ending_number; i++) (
int number = i;
int sqrt = (int) Math.sqrt(number);
if (sqrt * sqrt == number) (
System.out.println(number+ " = "+sqrt+"*"+sqrt);
)
)
)
)
Produktion:
Exempel 5
I detta program kommer vi att se summan av kvadrater för de första naturliga N-numren. Vi anger värdet på N och programmet beräknar summan av kvadraterna för de första naturliga N-numren.
Koda:
// Java Program to find sum of
// square of first n natural numbers
import java.io.*;
class SumofSquares
(
// Return the sum of the square of first n natural numbers
static int square sum(int n)
(
// Move the loop of I from 1 to n
// Finding square and then adding it to 1
int sum = 0;
for (int i = 1; i <= n; i++)
sum += (i * i);
return sum;
)
// Main() used to print the value of sum of squares
public static void main(String args()) throws IOException
(
int n = 6;
System.out.println("The sum of squares where N value is 6 is "+ squaresum(n));
)
)
Produktion:

Slutsats
- I den här artikeln ser vi en lista över metoder med vilka vi kan kvadratera ett nummer, hur vi kan hitta om ett tal är kvadratiskt eller inte inom ett specifikt intervall och även summan av heltal för de första naturliga N-numren. Men det finns också några andra tekniker som kan användas för att hitta kvadratet för ett nummer. Namnet på en teknik som kan användas för att se och kontrollera om ett tal är kvadratiskt eller inte är rekursionstekniken som använder en funktion inom en funktion för att kontrollera om numret är ett perfekt fyrkant eller inte.
- Även om rekursionstekniken är svår att använda, kan den användas för att beräkna kvadratet på ett tal inom några kodrader. Vidare kan vi med fyrkantiga nummer generera många mönsterprogram. Vi kan skriva ut ett fyrkantigt mönster i spiralformat eller i sicksackformat. På liknande sätt kan kvadratnumren användas i källkoden för att generera det dubbla kvadratet, såsom numret 16 där det dubbla kvadratet är nummer 2.
Rekommenderade artiklar
Detta är en guide till rutorna i Java. Här har vi diskuterat introduktionen längs exempel och koder med Output of Squares i Java. Du kan också gå igenom våra andra artiklar som föreslås för att lära dig mer–
- Mönster i Java
- Cheat Sheet JavaScript
- Vad är webbapplikation?
- Typer av webbhotell
- Square Root i PHP
- Arrays i Java-programmering
- Working and Top 3 Enum Methods in C #
- Square Root i JavaScript