Introduktion till hierarkisk klusteralgoritm
Den hierarkiska klusteralgoritmen är en maskinövervakningsteknik utan övervakning. Det syftar till att hitta en naturlig gruppering baserad på dataens egenskaper.
Den hierarkiska klusteralgoritmen syftar till att hitta kapslade grupper av data genom att bygga hierarkin. Det liknar den biologiska taxonomin i växt- eller djurriket. Hierarkiska kluster representeras vanligtvis med hjälp av det hierarkiska trädet som kallas ett dendrogram.
Typer av hierarkisk klusteralgoritm
Hierarkiska klusteralgoritmer är av två typer:
- splitt
- agglomerativ
1. Divisive
Detta är en ovanifrån och ner metod, där den initialt betraktar hela data som en grupp och sedan iterativt delar upp data i undergrupper. Om numret på en hierarkisk klusteralgoritm är känd, stoppar delningsprocessen när antalet kluster har uppnåtts. Annars slutar processen när data inte kan delas mer, vilket innebär att undergruppen som erhålls från den aktuella iterationen är densamma som den som erhållits från den föregående iterationen (man kan också överväga att uppdelningen stannar när varje datapunkt är ett kluster ).
2. Agglomerativ
Det är en bottom-up-strategi som bygger på sammanslagning av kluster. Ursprungligen delas uppgifterna i m singleton-kluster (där värdet på m är antalet sampel / datapunkter). Två kluster sammanfogas till en iterativt, vilket minskar antalet kluster i varje iteration. Denna process med sammanslagning av kluster slutar när alla kluster har släppts samman till ett eller antalet önskade kluster uppnås.
På nivå 1 finns det m-kluster som reduceras till 1 kluster på nivå m. De datapunkter som slås samman för att bilda ett kluster på en lägre nivå förblir också i samma kluster på de högre nivåerna. Antag att det finns 8 punkter x1..x8, så från början finns det 8 kluster på nivå 1. Anta att punkterna x1 och x2 slås samman i ett kluster på nivå 2, sedan till nivå 8, de stannar i samma kluster.
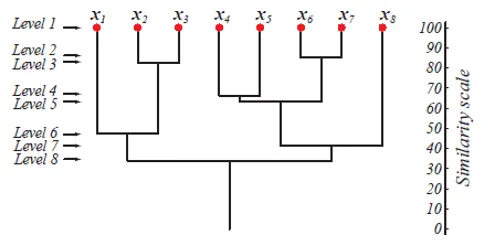
Ovanstående figur visar en dendrogramrepresentation av agglomerationsklusteringsmetoden för 8 datapunkter såväl som likhetsskalan motsvarande varje nivå.
Nivåerna av kluster ger oss en uppfattning om hur lika datapunkterna i klustren är. Som visas i fig 1, samlas tidigare datapunkterna i ett kluster, desto liknande är de. Så datapunkterna i ett kluster på nivå 2 (t.ex. x2 och x3) är mer lika än de datapunkter i ett kluster på nivå 6 (t.ex. x1 och x2).
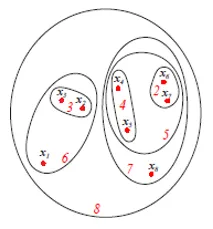
Figuren ovan visar Set- eller Venn-diagrammet som representerar den agglomerativa klusterinriktningen för de ovannämnda 8 datapunkterna. Både dendrogram och setrepresentationer kan användas för kluster. Men ett dendrogram är vanligtvis att föredra tillgångsrepresentation kan inte kvantitativt representera klusterlikheterna.
Steg för hierarkisk klusteralgoritm
Låt oss följa följande steg för den hierarkiska klusteralgoritmen som ges nedan:
1. Algoritm
Agglomerativ hierarkisk klusteralgoritm
- Börja initiera c, c1 = n, Di = (xi), i = 1, …, n '
- Gör c1 = c1 - 1
- Hitta närmaste kluster, säg Di och Dj
- Slå samman Di och Dj
- Tills c = c1
- Returnera c-kluster
- Slutet
Denna algoritm börjar med n kluster initialt där varje datapunkt är ett kluster. Med varje iteration minskar antalet kluster med 1 när de 2 närmaste klusteren slås samman. Denna process fortsätter tills antalet kluster minskar till det fördefinierade värdet c.
Hur bestämmer jag vilka kluster som är nära?
Det definieras med hjälp av flera avståndsmätningar som är följande:
- Det minsta avståndet mellan klusterna dmin (Di, Dj). Användbar för singel.
- Det maximala avståndet mellan klusterna dmax (Di, Dj). Användbart för komplett.
- Det genomsnittliga avståndet mellan klusterna davg (Di, Dj).
Vad är enkel länk och komplett länk?
- När dmin (di, dj) används för att hitta avståndet mellan två kluster, och algoritmen avslutas om avståndet mellan närmaste kluster överskrider en tröskel, kallas algoritmen en enda kopplingsalgoritm.
- När dmax (Di, Dj) används för att hitta avståndet mellan två kluster, och algoritmen avslutas om avståndet mellan närmaste kluster överskrider en tröskel, kallas algoritmen för en komplett kopplingsalgoritm.
- Låt oss betrakta varje datapunkt som en nod i en graf. Det finns en kant mellan två datapunkter om de tillhör samma kluster. När två närmaste kluster sammanfogas läggs en kant till. Det kallas en enda koppling eftersom det finns en unik sökväg från en nod till en annan.
- Den kompletta kopplingsalgoritmen sammanfogar två kluster genom att minimera avståndet mellan de två längsta punkterna.
- En enda kopplingsalgoritm genererar ett spännande träd. Denna algoritm är emellertid mottaglig för brus. En komplett kopplingsalgoritm genererar en komplett graf.
Vad är tidskomplexiteten hos algoritmen?
Anta att vi har n mönster i d-dimensionellt utrymme, och vi använder dmin (Di, Dj) för att bilda c-kluster. Vi måste beräkna n (n - 1) mellanpunktsavstånd - var och en är en O (d 2 ) beräkning - och placera resultaten i en interpunktsavståndstabell. Rymdkomplexiteten är O (n 2 ). Att hitta minsta avståndspar (för den första sammanslagningen) kräver att vi går igenom hela listan och håller indexet för det minsta avståndet.
För det första agglomerativa steget är således komplexiteten O (n (n - 1) (d2 + 1)) = O (n 2 d2). För ytterligare ett godtyckligt agglomerationssteg (dvs från c1 till c1 - 1) går vi bara igenom n (n - 1) - c1 "oanvända" avstånd i listan och hittar de minsta för vilka x och x 'ligger i olika kluster . Detta är återigen O (n (n − 1) −c1). Den totala tidskomplexiteten är sålunda O (cn 2 d 2 ) och under typiska förhållanden är n >> c.
2. Visualisering
När uppgifterna har delats upp i kluster är det en bra praxis att visualisera klustren för att få en uppfattning om hur ser gruppering ut. Men att visualisera dessa högdimensionella data är svårt. Därför använder vi Principal Component Analysis (PCA) för visualisering. Efter PCA erhåller vi datapunkterna i det låga dimensionella utrymmet (vanligtvis 2D eller 3D) som vi kan plotta för att se gruppering.
Obs: Hög dimension betyder ett stort antal funktioner och inte ett antal datapunkter.3. Utvärdering
En av metoderna för utvärdering av kluster är att avståndet mellan punkterna mellan klustren (inter-klusteravstånd) borde vara mycket mer än avståndet mellan punkterna inom klustret (intracluster avstånd).
Slutsats
Följande är några viktiga takeaways:
- Den hierarkiska klusteralgoritmen används för att hitta kapslade mönster i data
- Hierarkisk klustering är av två typer - Divisive och Agglomerative
- Dendrogram och set / Venn-diagram kan användas för representation
- Enkelkoppling sammanfogar två kluster genom att minimera minimiavståndet mellan dem. Det bildar en sträckning
- Komplett koppling sammanfogar två kluster genom att minimera det maximala avståndet mellan Det bildar en komplett graf.
- Den totala tidskomplexiteten för hierarkisk klusteralgoritm är O (cn 2 d 2 ), där c är det fördefinierade antalet kluster, n är antalet mönster och d är det d-dimensionella utrymmet för n-mönstren.
Rekommenderade artiklar
Detta är en guide till den hierarkiska klusteralgoritmen. Här diskuterar vi typer och steg i hierarkiska klusteralgoritmer. Du kan också titta på följande artiklar för att lära dig mer-
- Hierarkisk klusteranalys
- Hierarkisk klustering i R '
- Clustering algoritm
- Vad är Clustering i Data Mining?
- Hierarkisk klustering Agglomerativ & delande kluster
- C ++ algoritm | Exempel på C ++ -algoritm