
Introduktion till Fibonacci-serien i Python
Fibonacci-serien i Python, detta kallas en serie av nummer, där nästa nummer är summan av de nuvarande två siffrorna.
Till exempel:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. så vidare
Så här 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 och så vidare.
Ser man på ovanstående skulle man ha fått en viss uppfattning om vad vi pratar om.
När det gäller matematisk regel kan det emellertid skrivas som:

Där det nionde numret är summan av antalet på platser (n-1) och (n-2). När det gäller att implementera Fibonacci-serien kan det finnas ett antal kodningsspråk genom vilka det kan göras.
Men Python är ett allmänt använt språk idag. Låt oss se implementeringen av Fibonacci-serien genom Python. Man bör vara medveten om grundläggande konditioneringssatser som loopen, om-annars, medan-loopen etc. i Python, innan du fortsätter här. Om inte, skulle det vara bra om man kan revidera det och sedan ta upp det kommande innehållet. Här för demoändamål använder jag spyder som är IDE för programmeringsspråk för python. Man kan också använda alla andra IDE- eller Ipython-bärbara datorer för körning av Python-programmen.
Fibonacci-serien i Python
Låt oss se genomförandet av Fibonacci-nummer och serier med tanke på första två delar av Fibonacci är 0 och 1:
Du kan dock finjustera Fibonacci-funktionen enligt dina krav men se grunderna först och gradvis gå vidare till andra.
Python-kod för att hitta nionde Fibonacci-nummer
Kod 1:
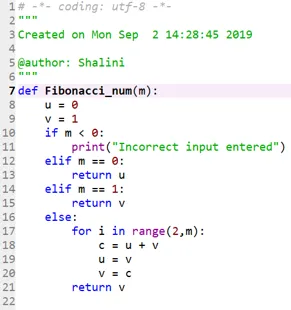
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Kod 2:
Produktion:
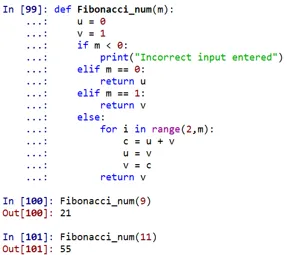
Som man kan se skulle Fibonacci-numret på nionde plats vara 21 och på 11: e plats 55.
- Här är "Chart_num" en definierad funktion som tar hand om att hitta Fibonacci-numret med hjälp av vissa villkor. Denna funktion kan anropas genom att ange vilken position som helst.
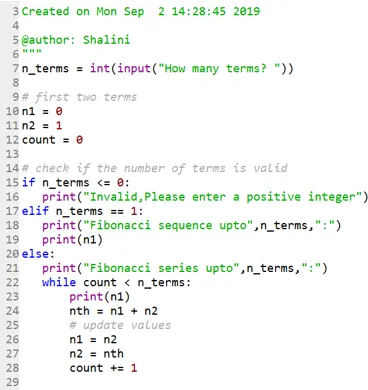
Låt oss nu se hur man kan skriva ut serier tills den nämnda positionen:
Koda:
Produktion:
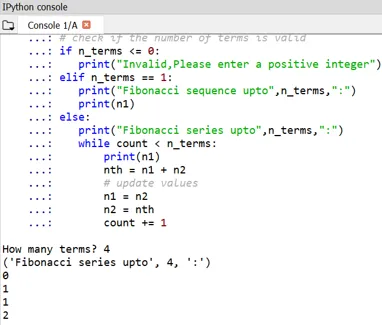
Man kan märka att starten av Fibonacci-nummer definieras som 0 och 1.
- Om någon vill definiera sina egna starttermer kan det också göras på samma sätt genom att finjustera n1 och n2. Här är exemplet för det:
Låt oss säga nu att vi vill att våra starttermer ska vara: n1 = 3, n2 = 5
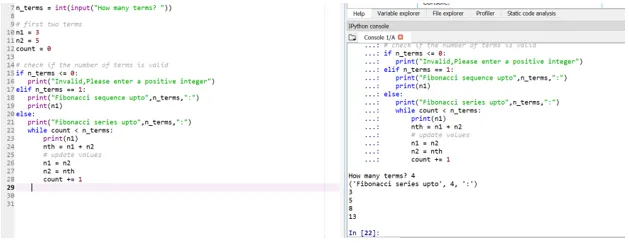
Så här kommer din fjärde terminposition (användarinmatning tas) att bestämmas utifrån dina startvillkor.
Metoder genom vilka Fibonacci-serien kan genereras
Nedan är de tre metoderna, genom vilka Fibonacci-serien kan genereras:
1. Genom generatorer
Koda:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Produktion:
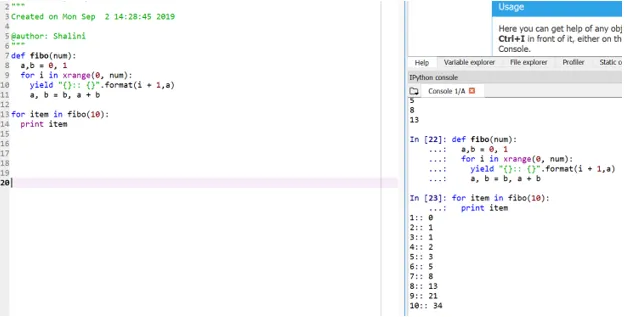
Denna metod kallas "generator" eftersom funktionen xrange är en generator med siffrorna mellan 0 och num och utbytet är generatorn för formaterad utgång.
Här är vad xrange gör för dig:

Här har Fibonacci-serien definierats i form av funktion, inuti vilken för loop-, xrange- och avkastningsfunktion tar hand om utgången.
2. Genom för slinga
Koda:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Produktion:

Som man kan se, har enkel för loop använts, för att skriva ut Fibonacci-serien mellan 0 till 10. Inuti slingan har nya värden tilldelats variablerna. U och v är standardvärdena för Fibonacci som har ställts in till 0 respektive 1.
När det gäller loop fortskrider att köra, är det nya u-värdet det gamla v-värdet, medan det nya v-värdet är summan av gamla värden på u och v. Detta fortsätter till slutet av intervallvärdena.
3. Genom rekursion
Koda:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Produktion:
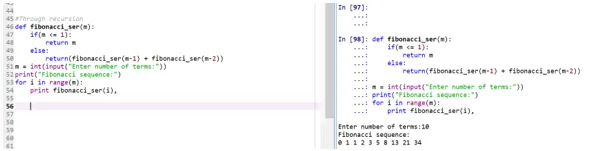
- Funktionen "retracement_ser" ringer till sig själv att skriva ut Fibonacci-serien.
- Och därmed har metoden fått sitt namn "rekursion".
Steg följs här:
- Här har användaren uppmanats att mata in platsen till vilken Fibonacci-serien behöver skrivas ut.
- Nummer går igenom funktionen ”retracement_ser”.
- Villkoret kontrolleras om den angivna längden är mindre än 1 eller inte. Om ja, ges resultatet omedelbart.
- Men om längden är större än 1 görs rekursiva samtal till "retracement_ser" med argument som har längd mindre än 1 och 2, dvs. retracement_ser (m-1) och retracement_ser (m-2).
- Därför ger rekursion önskad utskrift och skriver ut den.
- Så kort sagt, vi diskuterade tre sätt att visa Fibonacci-serien.
- Genom för slinga, genom generatorer och genom rekursion.
Alla tre Python-koderna sammanfattas
Nedan visas de tre pytonkoderna:
1. Genom generatorer
Koda:
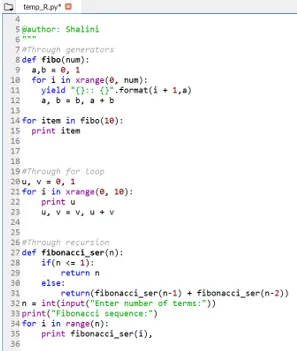
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Genom för slinga
Koda:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Genom rekursion
Koda:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Sammanfattat ovan är alla procedurer, man måste öva för att få ett bra grepp om alla.
Produktion:
Slutsats
Genom att gå igenom ovanstående innehåll i Fibonacci skulle man ha fått kristallklar förståelse av Fibonacci-nummer och serier, specialiserade på python. En gång blir man bekväm med Fibonacci-seriens logik, att generera en annan uppsättning serier, arbeta med andra nummer och med olika metoder kommer nu att vara en cakewalk för dig. En logisk metod är det enda sättet att utmärka sig i detta.
Rekommenderade artiklar
Detta är en guide till Fibonacci-serien i Python. Här diskuterar vi Fibonacci-nummer och -serier, specialiserade med python, genererar en annan uppsättning serier, arbetar med andra nummer och med olika metoder. Du kan också gå igenom våra andra relaterade artiklar för att lära dig mer -
- Random Number Generator i Python
- Matematikfunktioner i Python
- Factorial i Python
- Inkapsling i Python
- Fibonacci-serien i Java
- Python-funktioner
- Factorial-program i JavaScript
- Slumpmässig nummergenerator i Matlab
- Slumptalsgenerator i C #
- Inkapsling i JavaScript