Vägt genomsnittlig formel (innehållsförteckning)
- Vägt medelformel
- Vägt genomsnittskalkylator
- Vägt genomsnittlig formel i Excel (med Excel-mall)
Vägt medelformel
Formeln för beräkning av viktat genomsnitt är som följer:
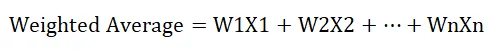
Var,
- W anger relativ vikt (i%)
- X anger värde
Exempel på viktad genomsnittlig formel
Låt oss se några exempel för att förstå viktad genomsnittlig formel:
Exempel 1
Låt oss anta att Anand har investerat pengarna i följande proportionerliga: 40% i investering A, 20% i investering B och 40% i investering C. Dessa investeringar har en avkastning på följande sätt: Investering A som 15%, investering B som 10 % och Investment C som 20%. Vi måste beräkna ett viktat genomsnitt för de avkastningskurser Anand skulle få.
Här,
- Vi har relativa vikter för investeringarna A, B & C som 40%, 20% respektive 40%.
- Och värde (avkastningskurs) för investeringarna A, B & C som 15%, 10% respektive 20%.
Genom att använda den viktade genomsnittliga formeln får vi-
- Vägt medelvärde = W1 X1 + W2 X2 + …… + Wn Xn
- Vägt medelvärde = 40% * 15% + 20% * 10% + 40% * 20%
- Vägt medelvärde = 16%
Detta visar att Anand kommer att erhålla 16% viktmedelvärdesavkastning från investeringarna A, B & C.
Exempel 2
Låt oss anta att Anand har anmält sig till en matematik-kurs, hans slutbetyg bestäms utifrån följande kategorier: test 30%, slutprov 40%, frågesporter 15% och läxor 15%.
Anand har fått följande betyg i varje kategori: Tester-80, Slutprov-65, frågesporter-85, läxor-90. Nu måste vi ta reda på Anands totala betyg.
För att beräkna ett viktat genomsnitt med procenttal måste varje kategorivärde först multipliceras med dess procentandel. Då måste alla dessa nya värden läggas samman.
Här,
Vi har relativa vikter för följande kategorier enligt följande:
- Test 30%
- Slut tentamen 40%
- frågesporter 15%
- läxor 15%
Och värde (märken) för kategorierna som
- Test-80
- Avslutande tentamen-65,
- frågesporter-85
- läxor-90
Genom att använda den viktade genomsnittliga formeln får vi-
- Vägt medelvärde = W1 X1 + W2 X2 + …… + WnXn
- Vägt medelvärde = (30% * 80) + (40% * 65) + (15% * 85) + (15% * 90)
- Vägt medelvärde = 76, 25 eller 76%
Detta visar den totala graden av Anand är 76%.
Exempel 3
Låt oss anta att Jagriti har investerat pengar i aktier i olika företag. Jagriti-portföljen omfattar 30% i lager A, 15% i lager B, 30% i lager C och de återstående 25% i lager D. Den förväntade avkastningen enligt den aktuella marknadssituationen för dessa aktier är följande: Avkastning på lager A är 15%, avkastning på lager B är 12%, avkastning på lager C är 17% och avkastning på lager D är 16%. Jagriti vill beräkna sin genomsnittliga avkastning på portföljen enligt den nuvarande marknadssituationen.
Här,
- Vi har relativa vikter på aktierna i portföljen enligt följande: A, B, C & D som 30%, 15%, 30% respektive 25%.
- Och värdet (avkastningskurs) för aktierna enligt följande: A, B, C & D som 15%, 12%, 17% respektive 16%.
Genom att använda den viktade genomsnittliga formeln får vi-
- Vägt medelvärde = W1 X1 + W2 X2 + W3 X3 + W4 X4 …… + Wn Xn
- Vägt medelvärde = (30% * 15%) + (15% * 12%) + (30% * 17%) + (25% * 16%)
- Vägt medelvärde = 0, 154 eller 15, 4%
Detta visar att Jagriti kommer att erhålla 15, 4% viktmedelvärdesavkastning från portföljen av aktierna A, B, C och D.
Förklaring av viktad genomsnittlig formel
Den vägda genomsnittliga formeln används för att beräkna medelvärdet för en viss uppsättning nummer med olika relevansnivåer. Vikterna måste representeras i termer av total relevans i procent. Vikterna bör vara lika med 100% eller 1.
För att beräkna viktad genomsnittlig formel behöver vi relativ vikt och värde.
Den första komponenten är Relativ viktning och den andra komponenten är värdeinmatningar. För att beräkna det viktade genomsnittet måste vi ha en specifik vikt för varje variabel som tas som värde och vikten måste vara lika med 100%.
Betydelse och användning av vägd genomsnittlig formel
Det vägda genomsnittet används i olika finansiella formler. Få exempel på vägt genomsnittligt beta och en vägd genomsnittlig kapitalkostnad (WACC).
Vi är bekanta med idén att hitta det athematiska medelvärdet eller genomsnittet för en serie artiklar. Vi kan helt enkelt lägga till värden på alla objekt och dela det med det totala antalet objekt för att beräkna medelvärdet. Detta fungerar bara om alla artiklar vägs lika. Till exempel, för att beräkna de genomsnittliga månatliga mobilräkningarna för ett år, kan vi helt enkelt lägga till de totala fakturerade beloppen för de senaste tolv månaderna och dela dem med tolv, då kan vi få en grov uppfattning om den genomsnittliga fakturan som har betalats, eftersom mobilen fakturacykeln är ungefär för samma tidsperiod, dvs. en månad.
Låt oss nu säga att du vill beräkna den aktuella genomsnittliga kursbetyget i din matematikklass. Vanligtvis tilldelar de flesta av klasserna olika vikt till tentamen än till läxuppgifter, interntest och tävlingar. I det här fallet måste du beräkna ett viktat medelvärde, som tar den specifika vikten för varje ämne för att beräkna din kursgrad.
Exempel på några fall där man måste använda ett viktat genomsnitt istället för ett enkelt medelvärde. Första fall- När vi vill beräkna ett genomsnitt som har olika procentvärden för olika kategorier. Ovanstående exempel på kursbetyget är ett liknande fall. Och för det andra när vi har en stor grupp artiklar med en annan regelbundenhet.
Om ett företag har en stor variation i försäljningen på grund av produktionen av en säsongsprodukt kan de använda den vägda genomsnittliga formeln. Och företaget vill beräkna genomsnittet för sina rörliga utgifter, då kan företaget använda den vägda genomsnittliga formeln och ta försäljningen som vikt för att få en bättre förståelse för sina utgifter. Och kan jämföra det belopp de producerar eller säljer.
Vägt genomsnittskalkylator
Du kan använda följande viktad genomsnittlig kalkylator
| W 1 | |
| X 1 | |
| W 2 | |
| X 2 | |
| W 3 | |
| X 3 | |
| W 4 | |
| X 4 | |
| Vägt medelformel | |
| Viktad genomsnittlig formel = | W 1 * X 1 + W 2 * X 2 + W 3 * X 3 + W 4 * X 4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Vägt genomsnittlig formel i Excel (med Excel-mall)
Här gör vi samma exempel på den viktade genomsnittliga formeln i Excel. Det är väldigt enkelt och enkelt. Du måste ange de två ingångarna, dvs. relativa vikter och avkastning.
Du kan enkelt beräkna det viktade genomsnittet med hjälp av formel i den medföljande mallen.
viktmedelsavkastning från investeringarna A, B & C beräknas som:

den totala graden av Anand beräknas som:

vikt Åldersgenomsnitt avkastning från portföljen av aktier A, B, C och D beräknas som:
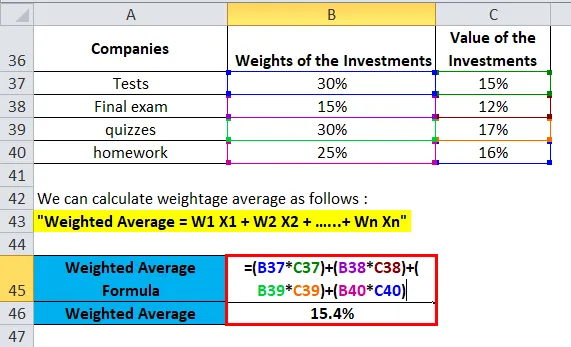
Du kan ladda ner denna viktade genomsnittliga formel Excel-mall här - Viktad genomsnittlig formel Excel-mall
Rekommenderade artiklar
Detta har varit en guide till en viktad genomsnittlig formel. Här diskuterar vi dess användning tillsammans med praktiska exempel. Vi ger dig också en viktad genomsnittlig kalkylator med nedladdningsbar Excel-mall. Du kan också titta på följande artiklar för att lära dig mer -
- Hur man beräknar omkostnaderna?
- Beräkna kapitalmultiplikator med exempel
- Användning av bruttovinstmarginalformel
- Handbok för beräkning av kundfordringar Omsättning