
Introduktion till rekursiv funktion i Java
En rekursiv funktion är den som kallar sig en eller flera gånger. En rekursiv funktion används i situationer där samma uppsättning operationer behöver utföras om och om igen tills resultatet har uppnåtts. Den utför flera iterationer och problemmeddelandet blir allt enklare med varje iteration.
Alltid måste en basgräns anges när du skriver en rekursiv funktion annars resulterar det i Stack Overflow-fel. En stack är ett minnesområde reserverat för att upprätthålla metodinokationer. Felet beror på att funktionen börjar köras kontinuerligt eftersom den inte kommer att kunna hitta det begränsande tillståndet och därmed slutligen uttömma det tilldelade minnet. Så för att förhindra Stack Overflow definierar vi vissa basförhållanden med hjälp av "if … else" -satser (eller andra villkorade uttalanden) som gör att rekursionsfunktionen stoppar så snart den beräknade beräkningen är klar.
Typer av rekursion i Java
Det finns två typer av rekursion i Java. Dom är:
1. Direkt rekursion
Syntax:
Här kallar funktionen sig själv kontinuerligt och är därför en rekursiv funktion.
public static void main(String() args)(
//few lines of code
function();
//few lines of code
)
function() (
//few lines of code
function();
//few lines of code
)
Exempel
Factorial för ett nummer är ett exempel på direkt rekursion. Den grundläggande principen för rekursion är att lösa ett komplicerat problem genom att delas upp i mindre. Till exempel, när det gäller faktoritet av ett tal, beräknar vi faktoriet för "i" om vi känner till dess faktorium för "i-1".
Koda:
public class Factorial (
static int fact(int i)(
if (i == 1)
return 1;
else
return(i * fact(i-1));
)
public static void main(String() args) (
System.out.println("The factorial of given number 6 is: "+fact(6));
)
)
Produktion:

2. Indirekt / ömsesidig rekursion
En funktion1 som kallar en annan funktion2, som i sin tur kallar funktion1 antingen direkt eller indirekt kallas en indirekt rekursiv funktion.
Syntax:
Överväg 2 funktioner som kallas funktion1 () och funktion2 (). Här kallar funktion1 funktion2 och funktion2 samtal funktion1.
function1()(
//few lines of code
function2();
//few lines of code
)
function2()(
//few lines of code
function1();
//few lines of code
)
Exempel
För att visa indirekt rekursion tar vi följande program som används för att ta reda på om ett givet antal är jämnt eller udda från den givna inmatningen.
Koda:
import java.util.Scanner;
public class IndirectRecursion (
public static boolean oddNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return false;
) else (
return evenNum(i-1);
)
)
public static boolean evenNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return true;
) else (
return oddNum(i-1);
)
)
public static void main(String() args) (
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
)
)
Produktion:
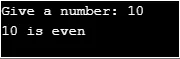
Exempel på rekursion i Java
Här är några fler exempel för att lösa problemen med rekursionsmetoden.
Exempel 1 - Fibonacci-sekvens
En uppsättning "n" -tal sägs vara i en Fibonacci-sekvens om nummer3 = nummer1 + nummer2, dvs varje nummer är en summa av dess föregående två siffror. Följaktligen börjar sekvensen alltid med de första två siffrorna som 0 och 1. Den tredje siffran är en summa av 0 och 1 vilket resulterar i 1, det fjärde talet är tillägget av 1 och 1 som resulterar i 2, och sekvensen fortsätter.
Kolla in följande kod i Java för att generera en Fibonacci-sekvens:
public class FibonacciSeries(
static int num1=0, num2=1, num3=0;
static void fibonacci(int n)(
if(n>0)(
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
)
)
public static void main(String args())(
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
)
)
Produktion:

Här initialiseras de två första siffrorna till 0 och 1 och skrivs ut. Variablerna "num1", "num2" och "num3" används för att generera den önskade sekvensen. Variabel "num3" erhålls genom att lägga till "num1" och "num2" och siffrorna flyttas en position till vänster genom att blanda som visas i koden. Funktionen "Fibonacci" kallas rekursivt här och vid varje iteration minskas värdet på "n" med 1. Därför kommer rekursionen ut så snart "n" når värdet 0.
Exempel # 2 - Tower Of Hanoi
Detta är ett klassiskt matematiskt problem som har 3 poler och ”n” antal skivor med olika storlekar. Pusslet går som följer:
I början kommer den första polen att ha skivorna ordnade så att den största skivan av dem alla är längst ner och den minsta på toppen av stången. Målet är att flytta dessa skivor från den första polen till den tredje polen och hålla skivorna i samma position som den i den första. Följande är några villkor att tänka på när du skifter dessa diskar:
1. Samtidigt måste bara en disk flyttas.
2. I processen är det inte tillåtet att placera en större disk över en mindre.
3. Den andra (mellersta) polen kan användas för att medla medan skivorna överförs från första till andra pol.
Följande är Java-koden som kan användas för att lösa pussel:
Koda:
public class TowerOfHanoi (
public static void main(String() args) (
int count = 3;
tower(count, 'A', 'B', 'C');
)
public static void tower(int first, char disk1, char temp, char disk2) (
if (first == 1) (
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
) else (
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
)
)
)
Produktion:
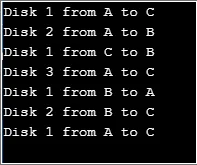
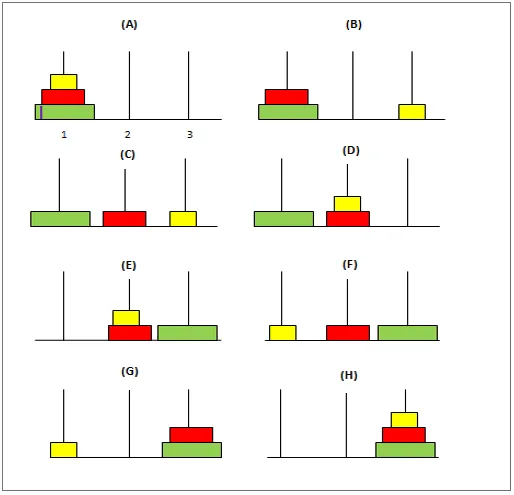
Här representerar variabeln "count" antalet skivor som ska användas. Funktionen “tornet” är den rekursiva funktionen som används för att flytta skivorna från stav 1 till stav 3. En enkel lösning på detta problem kan tillhandahållas genom att överväga två skivor till en början.
- Först börjar vi med att flytta skiva 1 från stav 1 till stav 2.
- Därefter flyttar vi skiva 2 till stav 3.
- Slutligen avslutar vi med att flytta skiva 1 till stav 3 för att slutföra den nödvändiga lösningen.
Samma princip tillämpas för "n" antalet skivor genom att flytta (n-1) skivan från stav 1 till 2 och följa liknande steg som ovan.
Fördelar med rekursion i Java
- Koden är lätt att skriva och underhålla.
- Den bästa metoden för att hitta resultaten där ett stort antal iterationer krävs.
Nackdelar med rekursion i Java
- Rekursiva funktioner använder mer minne. Detta beror på att varje gång en rekursiv funktion kallas; minnesallokering görs nyligen för variablerna på stacken. Och respektive minnesallokering frigörs så snart variabla värden returneras.
- Denna process för minnesallokering tar mer tid, varför utförandet vanligtvis är långsamt.
Slutsats
Rekursiva funktioner är relativt enkla att koda men de är inte heller så effektiva jämfört med de andra befintliga metoderna. Därför används de huvudsakligen i fall där tiden som ges för utveckling är mindre och även där ett betydande mönster kan observeras i problemet.
Rekommenderade artiklar
Detta är en guide till rekursion i Java. Här diskuterar vi typer av rekursion i Java tillsammans med dess olika exempel med fördelar och nackdelar. Du kan också titta på följande artiklar för att lära dig mer-
- JScrollPane i Java
- Matematikfunktioner i Java
- Matematikfunktioner i Java
- Konstruktör i Java
- Rekursiv funktion i Python
- Factorial-program i JavaScript