
Introduktion till exempel på standardavvikelser
Det finns gott om exempel på standardavvikelser. Standardavvikelse är måttet på spridningen av datasätt, dvs hur spridda siffrorna är. Det är användbart för att jämföra olika uppsättningar av data som kan ha samma medelvärde men olika intervall. Följande olika standardavvikelseexempel ger en förståelse för den vanligaste typen av situationer där standardavvikelsen beräknas och hur man kan beräkna samma
Exempel på standardavvikelse
Nedan följer exemplen på standardavvikelsen
Standardavvikelse - exempel # 1
Aktien i Company Z säljer för $ 50 per aktie och samma erbjudanden efter utbetalningar för nästa år:
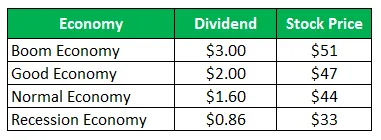
Beräkna standardavvikelsen när alla de fyra scenarierna ges är lika troliga.
Lösning:
Beräkningar av avkastning på innehavstid (HPR) är enligt följande -
Formel för HPR
HPR = ((Periodens slutvärde - originalvärde) + inkomst) / originalvärde) * 100
För Boom Economy
- HPR (Boom) = ((51-50) + 3) / 50 = 8, 00%
- HPR (Bra) = ((47-50) + 2) / 50 = -2, 00%
- HPR (Normal) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (lågkonjunktur) = ((33-50) + 0, 86) / 50 = -32, 28%
Beräkning av förväntad avkastning
Eftersom alla scenarier är lika troliga kommer sannolikheten för alla att vara ¼
Formel för förväntad återkomst
Förväntad avkastning = (Sannolikhet för bom * Retur från bom) + (sannolikhet för bra * återkomst från bra) + (sannolikhet för normal * återkomst från normal) + (sannolikhet för lågkonjunktur * återkomst från lågkonjunktur)
- Förväntad avkastning = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Förväntad avkastning = -8, 77%
Beräkning av standardavvikelse
Variationsformel
Varians = (Probability of Boom * (Return from Boom - Total Expected Return) 2) + (Probability of Good * (Return from Good - Total Expected Return) 2) + (Probability of Normal * (Return from Normal - Total Expected Return) 2 ) + (Sannolikheten för lågkonjunktur * (Återvändning från lågkonjunktur - Total förväntad återgång) 2)
- Varians = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Varians = 219, 95
Formel för standardavvikelse
Standardavvikelse kommer att vara kvadratrot av variation
Standardavvikelse = √Varians
- Standardavvikelse = √ 219, 95
- Standardavvikelse = 14, 83%
Exempel på standardavvikelse - 2
Standardavvikelse för två företag i portföljen
Företagets gemensamma aktie säljer för $ 28 per aktie och samma erbjudanden efter utbetalningar för nästa år

Den gemensamma aktien i företag B säljer för $ 93 per aktie och samma erbjudanden efter utbetalningar för nästa år:

(a) Beräkna standardavvikelsen för företag A
(b) Beräkna standardavvikelsen för företag B
(c) Beräkna portföljens standardavvikelse om hälften av investeringen görs är företag A och vila hälften i företag B
Lösning:
För företag A
Beräkningar av avkastning på innehavstid (HPR)
Formel för HPR
HPR = ((Periodens slutvärde - originalvärde) + inkomst) / originalvärde) * 100
- HPR (bom) = ((20-28) + 1) / 28 = -25, 00%
- HPR (Normal) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (lågkonjunktur) = ((38-28) + 5) / 28 = 53, 57%
Beräkning av förväntad avkastning för företag A
Formel för förväntad återkomst
Förväntad avkastning = (Sannolikhet för bom * Retur från bom) + (sannolikhet för normal * Retur från normal) + (sannolikhet för lågkonjunktur * Retur från lågkonjunktur)
- Förväntad avkastning = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Förväntad avkastning = 3, 84%
Beräkning av standardavvikelseföretag A
Variationsformel
Varians = (Probability of Boom * (Return from Boom - Total Expected Return) 2) + (Probability of Normal * (Return from Normal - Total Expected Return) 2 ) + (Probability of Recession * (Return from Recession - Total Expected Return)) 2)
- Varians = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Varians = 895, 15
Formel för standardavvikelse
Standardavvikelse kommer att vara kvadratrot av variation
Standardavvikelse = √Varians
- Standardavvikelse = √ 895.15
- Standardavvikelse = 29, 92%
För företag B
Beräkningar av avkastning på innehavstid (HPR)
Formel för HPR
HPR = ((Periodens slutvärde - originalvärde) + inkomst) / originalvärde) * 100
HPR (Boom) = ((200-93) +7) / 93 = 122, 58%
HPR (Normal) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (lågkonjunktur) = ((4-93) +2) / 93 = -93, 55%
Beräkning av förväntad avkastning
Formel för förväntad återkomst
Förväntad avkastning = (Sannolikhet för bom * Retur från bom) + (sannolikhet för normal * Retur från normal) + (sannolikhet för lågkonjunktur * Retur från lågkonjunktur)
- Förväntad avkastning = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Förväntad avkastning = 43, 04%
Beräkning av standardavvikelse
Variationsformel
Varians = (Probability of Boom * (Return from Boom - Total Expected Return) 2) + (Probability of Normal * (Return from Normal - Total Expected Return) 2 ) + (Probability of Recession * (Return from Recession - Total Expected Return)) 2)
- Varians = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Varians = 6783, 65
Formel för standardavvikelse
Standardavvikelse kommer att vara kvadratrot av variation
Standardavvikelse = √Varians
- Standardavvikelse = 676783, 65
- Standardavvikelse = 82, 36%
Beräkning av förväntad avkastning och standardavvikelse för en portföljhalva investerad i företag A och hälften i företag B.
Standardavvikelse för företag A = 29, 92%
Standardavvikelse för företag B = 82, 36%
Företagets vikt = 0, 50
Företagets vikt = 0, 50
Formeln för standardavvikelse för portfölj
Standardavvikelse för portfölj = (Företagets vikt * Förväntad avkastning på företag A) + ((Företagets vikt * Förväntad avkastning på företag B)
- Standardavvikelse för portfölj = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Standardavvikelse för portfölj = 56, 14%
Analys
Portföljens standardavvikelse är lägre än för endera aktiens individ eftersom aktierna är diversifierade i olika lager. Diversifiering leder till en minskning av risken såvida inte en perfekt korrelation finns mellan avkastningen på portföljinvesteringar.
Slutsats - Standardavvikelseexempel
Standardavvikelsen mäter spridningen av datasatsen som är relativt dess medelvärde. Det beräknas som varianskvadratroten. Ju större standardavvikelsen för säkerheten är, desto större blir variationen mellan var och en av priset och medelvärdet, vilket visar att prisintervallet är stort. Ovan nämnda exempel är några av exemplen på standardavvikelse på olika sätt. Det finns också flera andra exempel som visar att standardavvikelse kan beräknas med andra data.
Rekommenderade artiklar
Detta har varit en guide till standardavvikelseexemplen. Här diskuterar vi de olika exemplen på standardavvikelse tillsammans med en detaljerad förklaring . Du kan också titta på följande artiklar för att lära dig mer -
- Exempel på fasta kostnader
- Exempel på variabel kostnad
- Kvantitativt exempel
- Monopolistiska tävlingsexempel