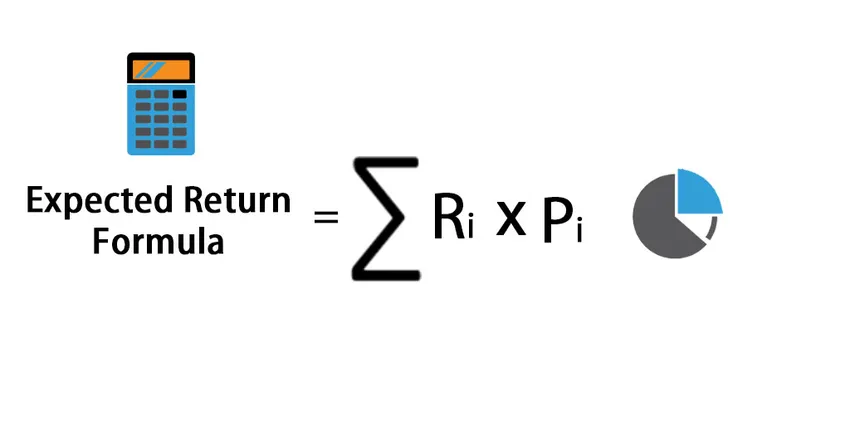
Förväntad returformel (innehållsförteckning)
- Förväntad returformel
- Exempel på förväntad returformel (med Excel-mall)
- Förväntad räkning för formelretur
Förväntad returformel
Förväntad avkastning kan definieras som den sannolika avkastningen för en portfölj som innehas av investerare baserat på tidigare avkastning eller det kan också definieras som ett förväntat värde på portföljen baserat på sannolikhetsfördelning av sannolik avkastning.
Här är den förväntade returformeln -
Expected Return = Expected Return=∑ (R i * P i )
Var
- R i - Return Förväntan på varje scenario
- P i - Sannolikheten för avkastningen i det scenariot
- i - Möjliga scenarier som sträcker sig från 1 till n
Exempel på förväntad returformel (med Excel-mall)
Låt oss ta ett exempel för att förstå beräkningen av formeln Expected Return på ett bättre sätt.
Förväntad returformel - exempel # 1
Låt oss ta ett exempel på en portfölj av aktier och obligationer där aktier har 50% och obligationer har en vikt på 50%. Den förväntade avkastningen på aktierna är 15% och den förväntade avkastningen för obligationer är 7%.
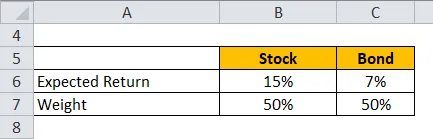
Förväntad avkastning beräknas med formeln nedan
Förväntad avkastning för portföljen = Aktiens vikt * Förväntad avkastning på lager + Obligationsvikt * Förväntad avkastning för obligationen
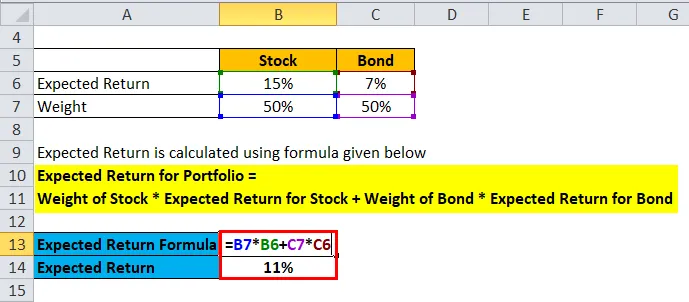
- Förväntad avkastning för portföljen = 50% * 15% + 50% * 7%
- Förväntad avkastning för portföljen = 7, 5% + 3, 5%
- Förväntad avkastning på portföljen = 11%
Förväntad returformel - exempel # 2
Låt oss ta ett exempel på portfölj som har stock Reliance, Tata Steel, Eicher Motors och ITC.
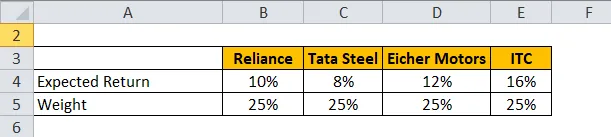
Förväntad avkastning beräknas med formeln nedan
Förväntad avkastning för portfölj = ∑ Vikt för varje aktie * Förväntad avkastning för varje aktie

- Förväntad avkastning på portfölj = 25% * 10% + 25% * 8% + 25% * 12% + 25% * 16%
- Förväntad avkastning för portföljen = 2, 5% + 2% + 3% + 4%
- Förväntad avkastning på portföljen = 11, 5%
Förväntad returformel - exempel # 3
Låt oss ta ett exempel på portfölj av HUL, HDFC och 10-årig statsobligation.
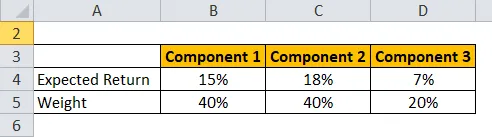
Förväntad avkastning beräknas med hjälp av formeln nedan
Förväntad avkastning för portfölj = ∑ Vikt för varje komponent * Förväntad avkastning för varje komponent
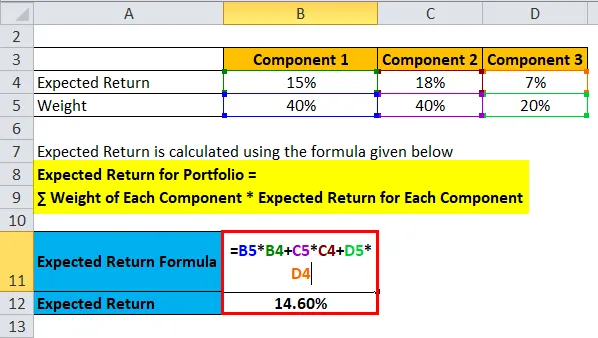
- Förväntad avkastning för portföljen = 40% * 15% + 40% * 18% + 20% * 7%
- Förväntad avkastning för portföljen = 6% + 7, 2% + 1, 40%
- Förväntad avkastning på portföljen = 14, 60%
Du kan ladda ner denna Expected Return Formula Excel Mall här - Expected Return Formula Excel Mall
Förklaring av förväntad returformel
Förväntad avkastning kan definieras som den sannolika avkastningen för en portfölj som innehas av investerare baserat på tidigare avkastning eller det kan också definieras som ett förväntat värde på portföljen baserat på sannolikhetsfördelning av sannolik avkastning. Den förväntade avkastningen kan ses på kort sikt som en slumpmässig variabel som kan ta olika värden baserade på vissa distinkta sannolikheter. Denna slumpmässiga variabel har värden inom ett visst intervall och kan endast ta värden inom det specifika intervallet. Därför är den förväntade avkastningsberäkningen baserad på historiska data och kan därför inte vara tillförlitlig när det gäller att förutse framtida avkastning. Det kan ses som ett mått på olika sannolikheter och sannolikheten för att få en positiv avkastning på sin investering och värdet på den avkastningen.
Syftet med detta är att ge en investerare en uppfattning om för en annan risknivå vad är de olika scenarierna med olika sannolikheter som ger en avkastning som är större än den riskfria avkastningen. Som vi alla vet, skulle den riskfria avkastningen vara den tioåriga statsobligationsräntan från USA: s regering.
Relevans och användningar av förväntad returformel
Som nämnts ovan baseras beräkningen på förväntad avkastning på historiska data och har därför en begränsning av att förutse framtida möjliga avkastning. Investerare måste komma ihåg olika andra faktorer och inte investera baserat på den beräknade avkastningen. Med ett exempel: -
Portfölj A - 10%, 12%, -9%, 2%, 25%
Portfölj B - 9%, 7%, 6%, 6%, 12%
Om vi beaktar båda ovanstående portföljer, har båda en förväntad avkastning på 8% men Portfölj A uppvisar mycket risk på grund av stor variation i avkastningen. Därför måste investerare ta hänsyn till denna risk som beräknas med mått som standardavvikelse och variation.
- Varians - Det kan definieras som en variation av en uppsättning datapunkter runt deras medelvärde. Det beräknas med det sannolikhetsviktade genomsnittet för kvadratiska avvikelser från medelvärdet. Det är ett mått på risk som investerare måste ta hänsyn till.
Först måste man beräkna medelvärdet för alla avkastningar. Sedan hittas varje avkastnings avvikelse från huvudvärdet och kvadreras för att säkerställa alla positiva resultat. Och när de är kvadrerade multipliceras de med respektive sannolikhetsvärden för att ta reda på variansen.
Portföljvarians kan beräknas med följande formel: - Om det finns två portföljer A och B
Portföljvariation = w A 2 * σ A 2 + w B 2 * σ B 2 + 2 * w A * w B * Cov (A, B)
Där Cov (A, B) - är samvariationen mellan portföljerna A och B
- Standardavvikelse - Det är en annan åtgärd som anger avvikelsen från dess medelvärde. Standardavvikelsen beräknas genom att ta en kvadratisk variansrot och betecknas med σ.
Förväntad räkning för formelretur
Du kan använda följande beräknade avkastningskalkylator.
| R 1 | |
| P 1 | |
| R 2 | |
| P 2 | |
| R 3 | |
| P 3 | |
| R 4 | |
| P 4 | |
| Förväntad retur | |
| Förväntad retur = | R 1 * P 1 + R 2 * P 2 + R 3 * P 3 + R 4 * P 4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Slutsats
Förväntad avkastning kan definieras som den troliga avkastningen för en portfölj som innehas av investerare baserat på tidigare avkastning. Eftersom det bara utnyttjar tidigare avkastning är det därför en begränsning och värdet på förväntad avkastning bör inte vara en enda faktor som investerare överväger när de beslutar om de ska investera i en portfölj eller inte. Det finns andra åtgärder som måste ses på, som portföljens variation och standardavvikelse.
Rekommenderade artiklar
Detta har varit en guide till formeln för förväntad retur. Här diskuterar vi hur man beräknar förväntad avkastning tillsammans med praktiska exempel. Vi tillhandahåller också Expected Return Calculator med nedladdningsbar Excel-mall. Du kan också titta på följande artiklar för att lära dig mer -
- Guide till formel för omsättningsgrad
- Guide till bud fråga spridning formel
- Hur beräknar jag kapacitetsutnyttjandegraden?
- Beräkning av obligationsekvivalentavkastning
- Formulär för omsättningsgrad | Exempel | Excel-mall