
Introduktion till Hashing-funktion i C
Den här artikeln har en kort anteckning om hashing (hash-tabell och hash-funktion). Det viktigaste konceptet är "sökning" som bestämmer tidskomplexiteten. För att minska tidskomplexiteten än någon annan datastruktur introduceras hashing-koncept som har O (1) -tid i genomsnittet och i värsta fall kommer det att ta O (n) -tid.
Hashing är en teknik med snabbare åtkomst till element som kartlägger den givna informationen med en mindre nyckel för jämförelser. I denna teknik spåras generellt tangenterna med hash-funktion i en tabell som kallas hash-tabellen.
Vad är Hash-funktion?
Hashfunktionen är en funktion som använder konstant-tid för att lagra och hämta värdet från hashtabellen, som tillämpas på tangenterna som heltal och den används som adress för värden i hashtabellen.
Typer av en Hash-funktion
Typerna av hashfunktioner förklaras nedan:
1. Uppdelningsmetod
I denna metod är hashfunktionen beroende av resten av en division.
Exempel: element som ska placeras i en hash-tabell är 42, 78, 89, 64 och låt oss ta tabellstorlek som 10.
Hash (nyckel) = Element% tabellstorlek;
2 = 42% 10;
8 = 78% 10;
9 = 89% 10;
4 = 64% 10;
Tabellrepresentationen kan ses som nedan:
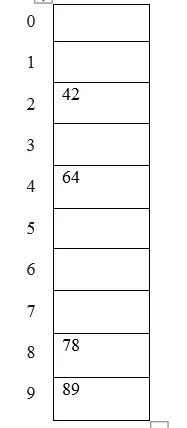
2. Mid Square-metoden
I den här metoden tas den mellersta delen av det kvadrerade elementet som index.
Elementet som ska placeras i hashbordet är 210, 350, 99, 890 och bordets storlek är 100.
210 * 210 = 44100, index = 1 som mittparti av resultatet (44100) är 1.
350 * 350 = 122500, index = 25 som mittparti av resultatet (122500) är 25.
99 * 99 = 9801, index = 80 som mittparti av resultatet (9801) är 80.
890 * 890 = 792100, index = 21 som mittparti av resultatet (792100) är 21.
3. Siffringsmetod
I denna metod är elementet som ska placeras i tabellen uh sing hash-tangenten, som erhålls genom att dela upp elementen i olika delar och sedan kombinera delarna genom att utföra några enkla matematiska operationer.
Element som ska placeras är 23576623, 34687734.
- hash (nyckel) = 235 + 766 + 23 = 1024
- hash-nyckel) = 34 + 68 + 77 + 34 = 213
I dessa typer av hashing antar vi att vi har siffror från 1- 100 och storleken på hashtabellen = 10. Element = 23, 12, 32
Hash (nyckel) = 23% 10 = 3;
Hash (nyckel) = 12% 10 = 2;
Hash (nyckel) = 32% 10 = 2;
I exemplet ovan märker du att båda elementen 12 och 32 pekar på 2: a platsen i tabellen, där det inte är möjligt att skriva båda på samma plats, ett sådant problem kallas en kollision. För att undvika denna typ av problem finns det några tekniker för hashfunktioner som kan användas.
Typer av kollisionsupplösningstekniker
Låt oss diskutera typerna av kollisionsupplösningstekniker:
1. Kedja
I den här metoden, som namnet antyder, tillhandahåller den en kedja med rutor för posten i tabellen med två poster av element. Så när sådana kollisioner inträffar, fungerar rutorna som en länkad lista.
Exempel: 23, 12, 32 med tabellstorlek 10.
Hash (nyckel) = 23% 10 = 3;
Hash (nyckel) = 12% 10 = 2;
Hash (nyckel) = 32% 10 = 2;
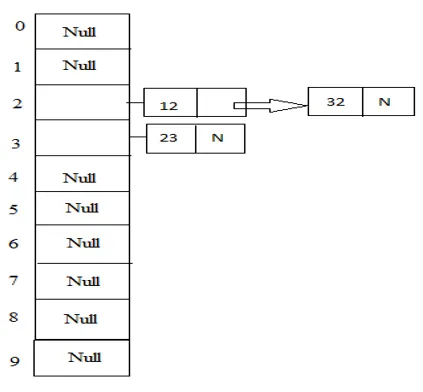
2. Öppna adressering
- Linjär probing
Detta är en annan metod för att lösa kollisionsproblem. Som namnet säger när en kollision inträffar bör två element placeras på samma post i tabellen, men med denna metod kan vi söka efter nästa tomma utrymme eller post i tabellen och placera det andra elementet. Detta kan åter leda till ett annat problem; om vi inte hittar någon tom post i tabellen leder det till kluster. Således är detta känt som ett klusterproblem, som kan lösas med följande metod.
Exempel: 23, 12, 32 med tabellstorlek 10
Hash (nyckel) = 23% 10 = 3;
Hash (nyckel) = 12% 10 = 2;
Hash (nyckel) = 32% 10 = 2;

I detta diagram kan 12 och 32 placeras i samma post med index 2 men med denna metod placeras de linjärt.
- Kvadratisk sondering
Denna metod är en upplösning för klusterproblemet under linjär sondering. I den här metoden beräknas hashfunktionen med hash-tangenten som hash (nyckel) = (hash (nyckel) + x * x)% av tabellens storlek (där x = 0, 1, 2 …).
Exempel: 23, 12, 32 med tabellstorlek 10
Hash (nyckel) = 23% 10 = 3;
Hash (nyckel) = 12% 10 = 2;
Hash (nyckel) = 32% 10 = 2;

I detta kan vi se att 23 och 12 enkelt kan placeras men 32 kan inte heller 12 och 32 delar samma post med samma index i tabellen, enligt denna metod hash (nyckel) = (32 + 1 * 1) % 10 = 3. Men i detta fall placeras tabellinföring med index 3 med 23 så vi måste öka x-värdet med 1. Hash (nyckel) = (32 + 2 * 2)% 10 = 6. Så vi kan nu placera 32 i posten med index 6 i tabellen.
- Dubbel hashing
Den här metoden måste vi beräkna 2 hashfunktioner för att lösa kollisionsproblemet. Den första beräknas med en enkel uppdelningsmetod. Det andra måste uppfylla två regler; det får inte vara lika med 0 och poster måste undersökas.
- 1 (nyckel) = nyckel% storlek på tabellen.
- 2 (nyckel) = p - (tangentmod p), där p är primtal <tabellens storlek.
Exempel: 23, 12, 32 med tabellstorlek 10
Hash (nyckel) = 23% 10 = 3;
Hash (nyckel) = 12% 10 = 2;
Hash (nyckel) = 32% 10 = 2;
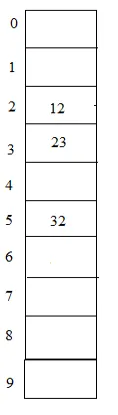
I detta igen kan elementet 32 placeras med hash2 (nyckel) = 5 - (32% 5) = 3. Så 32 kan placeras vid index 5 i tabellen som är tom eftersom vi måste hoppa 3 poster för att placera det.
Slutsats-Hashing-funktion i C
Hashing är en av de viktiga teknikerna när det gäller att söka data med mycket effektiva och snabba metoder med hashfunktion och hashtabeller. Varje element kan sökas och placeras med olika hashmetoder. Denna teknik är mycket snabbare än någon annan datastruktur när det gäller tidskoefficient.
Rekommenderade artiklar
Detta är en guide till Hashing-funktionen i C. Här diskuterar vi introduktionen av Hashing-funktionen i C, Vad är Hash-funktion, typer av en hash-funktion, etc. Du kan också gå igenom våra andra föreslagna artiklar för att lära dig mer–
- Hashing i DBMS
- Krypteringsprocess
- Hur installerar CakePHP?
- Hur Blockchain fungerar
- Hashing-funktion i Java
- Hashing-funktion i PHP | Hur man arbetar?